题目内容
(x2-
)3的展开式中常数项是( )
| 3 |
| x |
| A、9 | B、-9 | C、27 | D、-27 |
考点:二项式定理的应用
专题:二项式定理
分析:利用展开式的通项公式求出展开式的通项,令x的指数为0,求出r的值,求出答案.
解答:
解:展开式的通项为Tr+1=
×x2(3-r)×(-1)r×3r×x-r=
×(-3)r×x6-3r,令6-3r=0⇒r=2,
∴(x2-
)3的展开式中常数项是T3=
×9=27.
故选:C.
| C | r 3 |
| C | r 3 |
∴(x2-
| 3 |
| x |
| C | 2 3 |
故选:C.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
下列与抛物线y=
x2具有公共焦点的双曲线( )
| 1 |
| 8 |
| A、A、16y2-32x2=1 | ||||
B、
| ||||
C、
| ||||
D、x2-
|
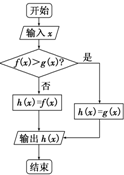
如图,若f(x)=logx3,g(x)=log2x,输入x=0.25,则输出h(x)=( )

| A、0.25 | ||
| B、2log32 | ||
C、-
| ||
| D、-2 |