题目内容
下列与抛物线y=
x2具有公共焦点的双曲线( )
| 1 |
| 8 |
| A、A、16y2-32x2=1 | ||||
B、
| ||||
C、
| ||||
D、x2-
|
考点:抛物线的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点坐标以及双曲线的焦点坐标,判断即可.
解答:
解:抛物线y=
x2的焦点坐标(0,2).焦点在y轴上,
双曲线
-
=1的焦点坐标(0,±2).
故选:B.
| 1 |
| 8 |
双曲线
| y2 |
| 2 |
| x2 |
| 2 |
故选:B.
点评:本题考查双曲线的焦点坐标的求法,抛物线的焦点坐标的求法,考查计算能力.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
在空间直角坐标系O-xyz中,一个四面体的顶点坐标为分别为(0,0,2),(2,2,0),(0,2,0),(2,2,2).画该四面体三视图中的正视图时,以xOz平面为投影面,则得到正视图可以为( )
A、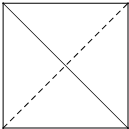 |
B、 |
C、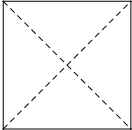 |
D、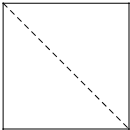 |
(x2-
)3的展开式中常数项是( )
| 3 |
| x |
| A、9 | B、-9 | C、27 | D、-27 |
已知f(x)=
是(-∞,+∞)上的增函数,那么实数a的取值范围是( )
|
| A、(0,3) | ||
| B、(1,3) | ||
| C、(1,+∞) | ||
D、[
|
已知线段PQ的两个端点的坐标分别为P(-1,6)、Q(2,2),若直线mx+y-m=0与线段PQ有交点,则实数m的取值范围是( )
| A、(-∞,-2]∪[3,+∞) |
| B、(-∞,-3]∪[2,+∞) |
| C、[-2,3] |
| D、[-3,2] |
已知命题p:x=1是方程ax2+bx+c=0的一个根,q:a+b+c=0,则命题p是命题q的( )
| A、充分不必要 |
| B、必要不充分 |
| C、既不充分又不必要 |
| D、充要 |
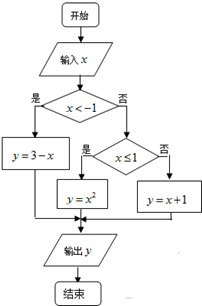 阅读右边的算法流程图(如图),解答下列问题:
阅读右边的算法流程图(如图),解答下列问题: 某市现有居民300万人,每天有1%的人选择乘出租车出行,记每个人的乘车里程为x(km),1≤x≤21.由调查数据得到x的频率分布直方图(如图),在直方图的乘车里程分组中,可以用各组在区间中点值代表该组的各个值,乘车里程落入该区间的频率作为乘车里程取该区间中点值的概率,现规定乘车里程x≤3时,乘车费用为10元;当x>3时,每超出1km(不足1km时按1km计算),乘车费用增加1.3元.
某市现有居民300万人,每天有1%的人选择乘出租车出行,记每个人的乘车里程为x(km),1≤x≤21.由调查数据得到x的频率分布直方图(如图),在直方图的乘车里程分组中,可以用各组在区间中点值代表该组的各个值,乘车里程落入该区间的频率作为乘车里程取该区间中点值的概率,现规定乘车里程x≤3时,乘车费用为10元;当x>3时,每超出1km(不足1km时按1km计算),乘车费用增加1.3元.