题目内容
函数f(x)=|sin
+cos
|+|sin
-cos
|-
在区间[-π,π]上的零点分别是 .
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 3 |
考点:余弦函数的图象,三角函数的周期性及其求法
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:令f(x)=|sin
+cos
|+|sin
-cos
|-
=0,可解得:|cosx|=
,由x∈[-π,π]即可解得在区间[-π,π]上的零点.
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 3 |
| 1 |
| 2 |
解答:
解:令f(x)=|sin
+cos
|+|sin
-cos
|-
=0
可得:
+
=
两边平方,得:2+2|cosx|=3,可解得:|cosx|=
,即cosx=±
∵x∈[-π,π]
∴x=
或-
或-
或
故答案为:
或-
或-
或
.
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 3 |
可得:
| 1+sinx |
| 1-sinx |
| 3 |
两边平方,得:2+2|cosx|=3,可解得:|cosx|=
| 1 |
| 2 |
| 1 |
| 2 |
∵x∈[-π,π]
∴x=
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
故答案为:
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
点评:本题主要考察了三角函数的图象与性质,函数的性质及应用,属于基本知识的考查.

练习册系列答案
相关题目
高二年级某研究性学习小组为了了解本校高一学生课外阅读状况,分成了两个调查小组分别对高一学生进行抽样调查.假设这两组同学抽取的样本容量相同且抽样方法合理,则下列结论正确的是( )
| A、两组同学制作的样本频率分布直方图一定相同 |
| B、两组同学的样本平均数一定相等 |
| C、两组同学的样本标准差一定相等 |
| D、该校高一年级每位同学被抽到的可能性一定相同 |
(x2-
)3的展开式中常数项是( )
| 3 |
| x |
| A、9 | B、-9 | C、27 | D、-27 |
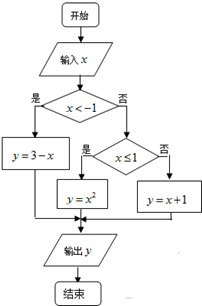 阅读右边的算法流程图(如图),解答下列问题:
阅读右边的算法流程图(如图),解答下列问题: 某市现有居民300万人,每天有1%的人选择乘出租车出行,记每个人的乘车里程为x(km),1≤x≤21.由调查数据得到x的频率分布直方图(如图),在直方图的乘车里程分组中,可以用各组在区间中点值代表该组的各个值,乘车里程落入该区间的频率作为乘车里程取该区间中点值的概率,现规定乘车里程x≤3时,乘车费用为10元;当x>3时,每超出1km(不足1km时按1km计算),乘车费用增加1.3元.
某市现有居民300万人,每天有1%的人选择乘出租车出行,记每个人的乘车里程为x(km),1≤x≤21.由调查数据得到x的频率分布直方图(如图),在直方图的乘车里程分组中,可以用各组在区间中点值代表该组的各个值,乘车里程落入该区间的频率作为乘车里程取该区间中点值的概率,现规定乘车里程x≤3时,乘车费用为10元;当x>3时,每超出1km(不足1km时按1km计算),乘车费用增加1.3元.