题目内容

棱长分别为3，4，5，的长方体的外接球的半径为
 
．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离,球
分析：由长方体与外接球的关系，即长方体的对角线长即为球的直径．列出方程，解得即可得到半径．
解答： 解：由长方体与外接球的关系，
即长方体的对角线长即为球的直径．
则有2r=
32+42+52
=5
2
，
则r=
5
2
2
．
故答案为：
5
2
2
点评：本题考查球与内接长方体的关系，考查长方体的对角线性质，考查运算能力，属于基础题．
练习册系列答案
相关题目
定义min[f（x），g（x）]=
f(x)，f(x)≤g(x)
g(x)，f(x)＞g(x)
，若函数f（x）=x2+tx+s的图象经过两点（x1，0），（x2，0），且存在整数m，使得m＜x1＜x2＜m+1成立，则（　　）
A、min[f（m），f（m+1）]＜
1
4
B、min[f（m），f（m+1）]＞
1
4
C、min[f（m），f（m+1）]=
1
4
D、min[f（m），f（m+1）]≥
1
4
已知f（x）=sin（2x+
π
6
）+sin（2x-
π
6
）+2cos2x+a，当x∈[-
π
4
，
π
4
]时，f（x）的最小值为-3，求a的值．
高二年级某研究性学习小组为了了解本校高一学生课外阅读状况，分成了两个调查小组分别对高一学生进行抽样调查．假设这两组同学抽取的样本容量相同且抽样方法合理，则下列结论正确的是（　　）
A、两组同学制作的样本频率分布直方图一定相同
B、两组同学的样本平均数一定相等
C、两组同学的样本标准差一定相等
D、该校高一年级每位同学被抽到的可能性一定相同
已知数列{an}满足a1=1，an=an-12-1（n＞1），写出它的前5项．
在空间直角坐标系O-xyz中，一个四面体的顶点坐标为分别为（0，0，2），（2，2，0），（0，2，0），（2，2，2）．画该四面体三视图中的正视图时，以xOz平面为投影面，则得到正视图可以为（　　）
A、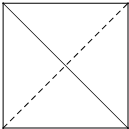
B、
C、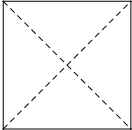
D、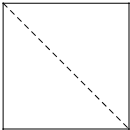
第一行是等差数列1，2，3…2013，将其相邻的两项和依次写下作为第二行，第二行相邻两项和依次写下作为第三行…依此类推，共写出12行，则各行第一个数之和为
 
．
求函数的单调区间：f（x）=-
1
3
x3+2x2-3x．
（x2-
3
x
）3的展开式中常数项是（　　）
A、9B、-9C、27D、-27

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网