题目内容
8.高三某班男同学有45名,女同学有15名,老师按照性别进行分层抽样组建了一个4人的课外兴趣小组.(1)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出一名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(2)试验结束后,第一次做试验的同学A得到的试验数据为68,70,71,72,74,第二次做试验的同学B得到的试验数据为69,70,70,72,74,请问哪位同学的实验更稳定?并说明理由.
分析 (1)设有x名男同学,列出方程求出男、女同学的人数分别为3、1,把3名男同学和1名女同学记为a1,a2,a3,b,由此利用列举法能求出选出的两名同学中恰有一名女同学的概率.
(2)分别求出平均数和方差,由此得到第二次同学B的实验更稳定.
解答 解:(1)设有x名男同学,则$\frac{45}{60}$=$\frac{x}{4}$,解得x=3,
∴男、女同学的人数分别为3、1,
把3名男同学和1名女同学记为a1,a2,a3,b,
则选取两名同学的基本事件有:
(a1,a2),(a1,a3),(a1,b),(a2,a1),(a2,a3),(a2,b),
(a3,a1),(a3,a2),(a3,b),(b,a1),(b,a2),(b,a3)共12种,
其中有一名女同学的有6种,
∴选出的两名同学中恰有一名女同学的概率为P=$\frac{6}{12}$=$\frac{1}{2}$.
(2)$\overline x$1=$\frac{68+70+71+72+74}{5}$=71,
$\overline x$2=$\frac{69+70+70+72+74}{5}$=71,
S12=$\frac{(68-71)2+…+(74-71)2}{5}$=4,
${{S}_{2}}^{2}$=$\frac{(69-71)2+…+(74-71)2}{5}$=3.2.
∴第二次同学B的实验更稳定.
点评 本题考查概率的求法,考查平均数、方差的求法及应用,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
16.已知$\frac{\overline z}{1+i}=2+i$,则复数z=( )
| A. | 1-3i | B. | -1-3i | C. | -1+3i | D. | 1+3i |
20.一个几何体的三视图如图所示,则该几何体的体积为( )
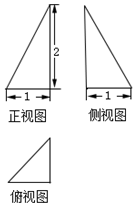

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
17.执行如图所示的程序框图,则输出的x等于( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
18.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据如表所示:
(1)求出y关于x的线性回归方程;
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
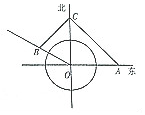 某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.
某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.