题目内容
19.△ABC中,a,b,c分别是角A,B,C的对边,设a+c=2b,A-C=$\frac{π}{3}$,则sinB的值为$\frac{\sqrt{39}}{8}$.分析 根据三角形内角和定理求出A、C的表达式,利用正弦定理化简a+c=2b,再由两角和与差、二倍角的正弦公式化简,即可求出sinB的值.
解答 解:△ABC中,A+B+C=π,
∴A+C=π-B,
又A-C=$\frac{π}{3}$,
∴A=$\frac{2π}{3}$-$\frac{B}{2}$,C=$\frac{π}{3}$-$\frac{B}{2}$;
又a+c=2b,
由正弦定理得:sinA+sinC=2sinB,
则sin($\frac{2π}{3}$-$\frac{B}{2}$)+sin($\frac{π}{3}$-$\frac{B}{2}$)=2sinB,
∴sin$\frac{2π}{3}$cos$\frac{B}{2}$-cos$\frac{2π}{3}$sin$\frac{B}{2}$+sin$\frac{π}{3}$cos$\frac{B}{2}$-cos$\frac{π}{3}$sin$\frac{B}{2}$=4sin$\frac{B}{2}$cos$\frac{B}{2}$
∴$\sqrt{3}$cos$\frac{B}{2}$=4sin$\frac{B}{2}$cos$\frac{B}{2}$,
由0<B<π得,0<$\frac{B}{2}$<$\frac{π}{2}$,∴cos$\frac{B}{2}$>0,
∴sin$\frac{B}{2}$=$\frac{\sqrt{3}}{4}$,cos$\frac{B}{2}$═$\sqrt{1{-(\frac{\sqrt{3}}{4})}^{2}}$=$\frac{\sqrt{13}}{4}$,
∴sinB=2sin$\frac{B}{2}$cos$\frac{B}{2}$=2×$\frac{\sqrt{3}}{4}$×$\frac{\sqrt{13}}{4}$=$\frac{\sqrt{39}}{8}$.
故答案为:$\frac{\sqrt{39}}{8}$.
点评 本题考查了正弦定理与三角形内角和定理,两角和与差、二倍角的正弦公式应用问题,是综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | $2+\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
| A. | 120种 | B. | 96种 | C. | 60种 | D. | 48种 |
①y=2x ②y=x2+2x-1 ③y=|x+2|④y=|x|+2.
| A. | ①② | B. | ①③ | C. | ②③④ | D. | ①②③④ |
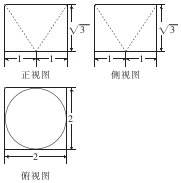
| A. | 8($\sqrt{3}$+1)+π | B. | 8($\sqrt{3}$+1)+2π | C. | 8($\sqrt{3}$+1)一π | D. | 8($\sqrt{3}$+l) |