题目内容
13．关于x的方程$1-kx=\sqrt{1-{{（x-2）}^2}}$有实根时，k的取值范围是[-1，0]．分析 可化为函数y=1-kx与函数y=$\sqrt{1-（x-2）^{2}}$的图象有交点，作图象求解
解答 解：关于x的方程$1-kx=\sqrt{1-{{（x-2）}^2}}$有实根?函数y=1-kx与函数y=$\sqrt{1-（x-2）^{2}}$的图象有交点，
函数y=$\sqrt{1-（x-2）^{2}}$的图象是圆（x-2）2+y2=1（y≥0）的部分，函数y=1-kx过定点（0，1），
其图象如下：结合图象可得k的取值范围是[-1，0]．
故答案为：[-1，0]
点评 本题考查了函数与方程思想、数形结合的思想应用，属于中档题．
练习册系列答案
相关题目
4．某几何体的三视图如图所示，则该几何体的表面积为（ ）
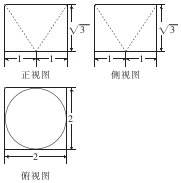
| A． | 8（$\sqrt{3}$+1）+π | B． | 8（$\sqrt{3}$+1）+2π | C． | 8（$\sqrt{3}$+1）一π | D． | 8（$\sqrt{3}$+l） |
1．已知实数x，y满足不等式组$\left\{\begin{array}{l}x-3y+5≥0\\ 2x+y-4≤0\\ y+2≥0\end{array}\right.$则z=x+y的最小值为-13．
5．顶点在原点，焦点在x轴上，且经过点P（-1，2）的拋物线的标准方程是（ ）
| A． | y2=$\frac{1}{4}$x | B． | y2=-$\frac{1}{4}$x | C． | y2=-4x | D． | x2=-4y |