题目内容
16.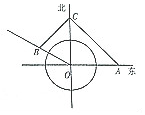 某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.
某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路,工厂正北方向有一观察站C,OC=2千米,因化工厂原料泄漏,工厂周围1千米的范围内均有不同程度的影响.现准备从观察站C处修两条隔离绿化带CA,CB(其中A,B为隔离带与公路交接点).且使CA⊥CB,隔离带与两条公路线围成的面积为S.(1)①若OA=a千米,试把S表示成a的函数.并写出其定义域;
②若∠OAC=θ,试把S表示成θ的函数,并写出其定义域;
(2)选择上述两个函数中的以个,试求S的最小值.
分析 (1)①设B(x,-$\sqrt{3}$x),根据BC⊥AC列方程解出x从而求出两个三角形的面积;
②利用正弦定理计算OB,得出三角形的面积;
(2)判断函数的单调性,利用单调性求出最小值;
解答 解:(1)①由题意可知∠BOC=$\frac{π}{3}$,∴直线OB的方程为y=-$\sqrt{3}$x,
设B(x,-$\sqrt{3}$x),则kBC=$\frac{2+\sqrt{3}x}{-x}$,kAC=$\frac{2}{-a}$,
∵BC⊥AC,∴$\frac{2+\sqrt{3}x}{-x}$•$\frac{2}{-a}$=-1,解得x=-$\frac{4}{2\sqrt{3}+a}$.
∴S△OBC=$\frac{1}{2}OC•|x|$=$\frac{4}{2\sqrt{3}+a}$,又S△AOC=$\frac{1}{2}OA•OC$=a,
∴S=$\frac{4}{2\sqrt{3}+a}$+a.
由题意可知当AC与圆O相切时,OA取的最小值,
设AC的最小值为m,则AC=$\sqrt{{m}^{2}+4}$,
∵OA•OC=AC•1,即2m=$\sqrt{{m}^{2}+4}$,∴m=$\frac{2\sqrt{3}}{3}$.
∴定义域为{a|a≥$\frac{2\sqrt{3}}{3}$}.
②∵BC⊥AC,∴∠BCO=∠OAC=θ,∴∠OBC=$\frac{2π}{3}$-θ,
在△OBC中,由正弦定理得$\frac{sin(\frac{2π}{3}-θ)}{2}=\frac{sinθ}{OB}$,
∴OB=$\frac{2sinθ}{sin(\frac{2π}{3}-θ)}$,∴S△OBC=$\frac{1}{2}$OB•OCsin$\frac{π}{3}$=$\frac{\sqrt{3}sinθ}{sin(\frac{2π}{3}-θ)}$,
又tanθ=$\frac{OC}{OA}=\frac{2}{OA}$,∴OA=$\frac{2}{tanθ}$,∴S△OAC=$\frac{1}{2}OA•OC$=$\frac{2}{tanθ}$,
∴S=$\frac{\sqrt{3}sinθ}{sin(\frac{2π}{3}-θ)}$+$\frac{2}{tanθ}$.
当θ取得最小值时,AC与圆O相切,∴θ的最大值为$\frac{π}{3}$.
∴定义域为{θ|0<θ≤$\frac{π}{3}$}.
(2)S(a)=$\frac{4}{2\sqrt{3}+a}+a$,S′(a)=1-$\frac{4}{(2\sqrt{3}+a)^{2}}$=$\frac{(2\sqrt{3}+a)^{2}-4}{(2\sqrt{3}+a)^{2}}$=$\frac{(2\sqrt{3}+a+2)(2\sqrt{3}+a-2)}{(2\sqrt{3}+a)^{2}}$,
∵a$≥\frac{2\sqrt{3}}{3}$,∴S′(a)>0,
∴S(a)在[$\frac{2\sqrt{3}}{3}$,+∞)上是增函数,
∴当a=$\frac{2\sqrt{3}}{3}$时,S(a)取得最小值S($\frac{2\sqrt{3}}{3}$)=$\frac{7\sqrt{3}}{6}$.
点评 本题考查了函数解析式的求解,函数单调性判断和最值的计算,属于中档题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | $2+\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
| A. | 120种 | B. | 96种 | C. | 60种 | D. | 48种 |
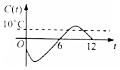
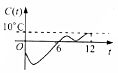
 某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )