题目内容

16．已知$\frac{\overline z}{1+i}=2+i$，则复数z=（　　）
A．1-3iB．-1-3iC．-1+3iD．1+3i

分析 利用复数的运算法则、共轭复数的定义即可得出．

解答 解：$\frac{\overline z}{1+i}=2+i$，∴$\overline{z}$=（1+i）（2+i）=1+3i．
则复数z=1-3i．
故选：A．

点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
4．已知两圆相交于A（-1，3），B（-6，m）两点，且这两圆的圆心均在直线x-y+c=0上，则m+2c的值为（　　）
A．-1B．26C．3D．2
7．从5个不同的小球中选4个放入3个箱子中，要求第一个箱子放入1个小球，第二个箱子放入2个小球，第三个箱子放入1个小球，则不同的放法共有（　　）
A．120种B．96种C．60种D．48种
4．某几何体的三视图如图所示，则该几何体的表面积为（　　）
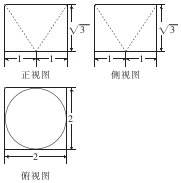
A．8（$\sqrt{3}$+1）+πB．8（$\sqrt{3}$+1）+2πC．8（$\sqrt{3}$+1）一πD．8（$\sqrt{3}$+l）
11．已知函数f（x）=|lnx|，g（x）=k（x-1）（k∈R）．
（1）若两个实数a，b满足0＜a＜b，且f（a）=f（b），求4a-b的取值范围；
（2）证明：当k＜1时，存在x0＞1，使得对任意的x∈（1，x0），恒有f（x）＞g（x）；
（3）已知0＜a＜b，证明：存在x0∈（a，b），使得$\frac{lnb-lna}{b-a}=\frac{1}{x_0}$．
1．已知实数x，y满足不等式组$\left\{\begin{array}{l}x-3y+5≥0\\ 2x+y-4≤0\\ y+2≥0\end{array}\right.$则z=x+y的最小值为-13．
8．高三某班男同学有45名，女同学有15名，老师按照性别进行分层抽样组建了一个4人的课外兴趣小组．
（1）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出一名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
（2）试验结束后，第一次做试验的同学A得到的试验数据为68，70，71，72，74，第二次做试验的同学B得到的试验数据为69，70，70，72，74，请问哪位同学的实验更稳定？并说明理由．
5．顶点在原点，焦点在x轴上，且经过点P（-1，2）的拋物线的标准方程是（　　）
A．y2=$\frac{1}{4}$xB．y2=-$\frac{1}{4}$xC．y2=-4xD．x2=-4y
6．已知双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0．b＞0），若矩形ABCD的四个顶点在E上，AB，CD的中点为双曲线E的两个焦点，且双曲线E的离心率是2．直线AC的斜率为k．则|k|等于（　　）
A．2B．$\frac{3}{2}$C．$\frac{5}{2}$D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网