题目内容
20．一个几何体的三视图如图所示，则该几何体的体积为（ ）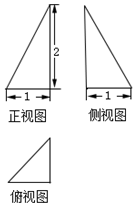
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | 1 |
分析 由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，并能分析出底面两直角边的长和棱锥的高，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥
底面是一个两直角边分别为1和1的直角三角形
故底面S=$\frac{1}{2}$×1×1=$\frac{1}{2}$
棱锥的高为h=2，
故棱锥的体积V=$\frac{1}{3}$Sh=$\frac{1}{3}$×$\frac{1}{2}$×2=$\frac{1}{3}$，
故选B．
点评 本题考查的知识点是由三视图求体积，其中由已知中的三视图判断出几何体的形状，及棱长，高等几何量是解答的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8．设F为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右焦点，过坐标原点的直线依次与双曲线C的左、右支交于点P，Q，若|PQ|=2|QF|，∠PQF=60°，则该双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | $1+\sqrt{3}$ | C． | $2+\sqrt{3}$ | D． | $4+2\sqrt{3}$ |
15．执行如图程序框图（见上图），如果输入的x，t均为2，S=（ ）
| A． | 7 | B． | 6 | C． | 5 | D． | 4 |
5．顶点在原点，焦点在x轴上，且经过点P（-1，2）的拋物线的标准方程是（ ）
| A． | y2=$\frac{1}{4}$x | B． | y2=-$\frac{1}{4}$x | C． | y2=-4x | D． | x2=-4y |