题目内容
3.把函数f(x)=$\sqrt{3}$cos2x-sin2x的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )| A. | [-$\frac{π}{2}$,0] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{2}$] |
分析 将函数函数f(x)=$\sqrt{3}$cos2x-sin2x化简为f(x)=2cos(2x+$\frac{π}{6}$),利用函数y=Asin(ωx+φ)的图象变换规律得到函数y=g(x)的图象,结合余弦函数的单调性可得结论.
解答 解:函数f(x)=$\sqrt{3}$cos2x-sin2x=2cos(2x+$\frac{π}{6}$),向右平移$\frac{π}{12}$个单位得到2cos(2(x$-\frac{π}{12}$)$+\frac{π}{6}$)=2cos2x=g(x),
由y=cosx的一个单调递减区间为[0,π],
∴g(x)=2cos2x的一个单调递减区间为[0,$\frac{π}{2}$],
故选D
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知P(x,y)为区域$\left\{\begin{array}{l}{y^2}-4{x^2}≤0\\ a≤x≤0\end{array}\right.$内的任意一点,当该区域的面积为4时,z=x-2y的最小值是( )
| A. | $-5\sqrt{2}$ | B. | $-3\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{12}$ |
18.如图所示,在△ABC内随机选取一点P,则△PBC的面积不超过△ABC面积一半的概率是( )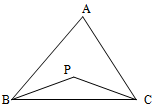

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
15.现有4人参加抽奖活动,每人依次从装有4张奖票(其中2张为中奖票)的箱子中不放回地随机抽取一张,直到2张中奖票都被抽出时活动结束,则活动恰好在第3人抽完后结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
13.已知a<b<0,则( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2<ab | C. | a2<b2 | D. | $\frac{1}{a-b}<\frac{1}{a}$ |