题目内容
5.已知tanx=-$\frac{1}{2}$,则2sinxcosx=( )| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
分析 由条件利用同角三角函数的基本关系,求得2sinxcosx的值.
解答 解:∵tanx=-$\frac{1}{2}$,
∴2sinxcosx=$\frac{2sinxcosx}{si{n}^{2}x+co{s}^{2}x}$=$\frac{2tanx}{1+ta{n}^{2}x}$=-$\frac{4}{5}$.
故选:A.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
15.已知P(x,y)为区域$\left\{\begin{array}{l}{y^2}-4{x^2}≤0\\ a≤x≤0\end{array}\right.$内的任意一点,当该区域的面积为4时,z=x-2y的最小值是( )
| A. | $-5\sqrt{2}$ | B. | $-3\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
15.现有4人参加抽奖活动,每人依次从装有4张奖票(其中2张为中奖票)的箱子中不放回地随机抽取一张,直到2张中奖票都被抽出时活动结束,则活动恰好在第3人抽完后结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
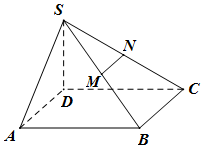 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.