题目内容
7.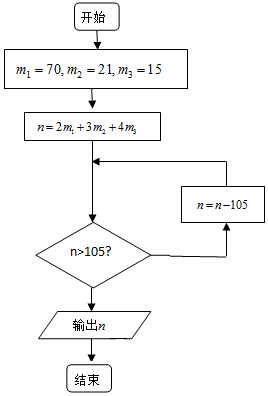 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
分析 【法一】根据正整数n被3除余2,被5除余3,被7除余4,求出n的最小值.
【法二】按此歌诀得算法的程序框图,按程序框图知n的初值,代入循环结构求得n的值.
解答 解:【法一】正整数n被3除余2,得n=3k+2,k∈N;
被5除余3,得n=5l+3,l∈N;
被7除余4,得n=7m+4,m∈N;
求得n的最小值是53.
【法二】按此歌诀得算法如图,
则输出n的结果为
按程序框图知n的初值为263,代入循环结构得n=263-105-105=53,
即输出n值为53.
故选:A.
点评 本题考查了程序框图的应用问题,也考查了古代数学的应用问题,是基础题.

练习册系列答案
相关题目
18.如图所示,在△ABC内随机选取一点P,则△PBC的面积不超过△ABC面积一半的概率是( )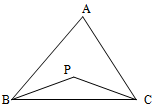

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
15.现有4人参加抽奖活动,每人依次从装有4张奖票(其中2张为中奖票)的箱子中不放回地随机抽取一张,直到2张中奖票都被抽出时活动结束,则活动恰好在第3人抽完后结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2.下列命题正确的是( )
| A. | “x<-2”是“x2+3x+2>0”的必要不充分条件 | |
| B. | 对于命题p:?x0∈R,使得${x_0}^2+{x_0}-1<0$,则¬p:?x∈R,均有x2+x-1≥0 | |
| C. | 命题“若x2-3x+2=0,则x=2”的否命题为若x2-3x+2=0,则x≠2 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
19.$\frac{{{i^{2017}}}}{1-2i}$=( )
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
17.在△ABC中,命题p:“B≠60°“,命题q:“△ABC的三个内角A,B,C不成等差数列“,那么p是q的
( )
( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |