题目内容
6.2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)根据题意计算喜欢游泳的学生人数,求出女生、男生有多少人,补充列联表即可;
(Ⅱ)计算观测值K2,对照临界值表即可得出结论.
解答 解:(Ⅰ)因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为$\frac{3}{5}$,
所以喜欢游泳的学生人数为$100×\frac{3}{5}=60$人;
其中女生有20人,男生有40人,列联表补充如下:
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(Ⅱ)因为K2=$\frac{100{×(40×30-20×10)}^{2}}{60×40×50×50}$≈16.67>10.828;
所以有99.9%的把握认为喜欢游泳与性别有关. …12分.
点评 本题考查了独立性检验与运算求解能力,是基础题.

练习册系列答案
相关题目
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的离心率为2,则该双曲线的渐近线方程为( )
| A. | x±y=0 | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{3}x±y=0$ | D. | 2x±y=0 |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{12}$ |
18.如图所示,在△ABC内随机选取一点P,则△PBC的面积不超过△ABC面积一半的概率是( )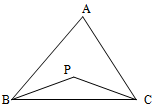

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
15.现有4人参加抽奖活动,每人依次从装有4张奖票(其中2张为中奖票)的箱子中不放回地随机抽取一张,直到2张中奖票都被抽出时活动结束,则活动恰好在第3人抽完后结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
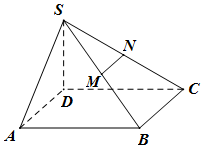 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.