题目内容
10.某公司在新年晚会上举行抽奖活动,有甲,乙两个抽奖方案供员工选择.方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为$\frac{4}{5}$,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则不能获得奖金.
方案乙:员工连续三次抽奖,每次中奖率均为$\frac{2}{5}$,每次中奖均可获得奖金400元.
(Ⅰ)求某员工选择方案甲进行抽奖所获奖金X(元)的分布列;
(Ⅱ)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
(Ⅲ)已知公司共有100人在活动中选择了方案甲,试估计这些员工活动结束后没有获奖的人数.
分析 (Ⅰ)由题意知X可能的取值为0,500,1000,分别求出相应的概率,由此能求出某员工选择方案甲进行抽奖所获奖金X(元)的分布列.
(Ⅱ)求出方案甲抽奖所获奖金X的均值,选择方案乙进行抽奖中奖次数ξ~B(3,$\frac{2}{5}$),从而抽奖所获奖金X′的均值E(X′)=E(400ξ)=400E(ξ)=480,由此得到选择方案甲较划算.
(Ⅲ)选择方案甲不获奖的概率为$\frac{7}{25}$,这些员工不获奖的人数Y~B(100,$\frac{7}{25}$),由此能求出这些员工不获奖的人数.
解答 解:(Ⅰ)由题意知X可能的取值为0,500,1000,(1分)
$P(X=0)=\frac{1}{5}+\frac{4}{5}•\frac{1}{2}•\frac{1}{5}=\frac{7}{25}$,
$P(X=500)=\frac{4}{5}•\frac{1}{2}=\frac{2}{5}$,
$P(X=1000)=\frac{4}{5}•\frac{1}{2}•\frac{4}{5}=\frac{8}{25}$(4分)
所以某员工选择方案甲进行抽奖所获奖金X(元)的分布列为
| X | 0 | 500 | 1000 |
| P | $\frac{7}{25}$ | $\frac{2}{5}$ | $\frac{8}{25}$ |
(Ⅱ)由(Ⅰ)知,方案甲抽奖所获奖金X的均值$E(X)=500•\frac{2}{5}+1000•\frac{8}{25}=520$,(6分)
若选择方案乙进行抽奖中奖次数ξ~B(3,$\frac{2}{5}$),
则$E(ξ)=3•\frac{2}{5}=\frac{6}{5}$,(8分)
抽奖所获奖金X′的均值E(X′)=E(400ξ)=400E(ξ)=480,
因边E(X)>E(ξ),
故选择方案甲较划算. (10分)
(Ⅲ)由(Ⅰ)知选择方案甲不获奖的概率为$\frac{7}{25}$,
这些员工不获奖的人数Y~B(100,$\frac{7}{25}$),
$E(Y)=100×\frac{7}{25}=28$,故这些员工不获奖的人数约为28人.(12分)
点评 本题考查离散型随机变量的分布列及数学期望的求法及应用,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
相关题目
20.已知α∈[$\frac{π}{2}$,$\frac{3π}{2}$],β∈[-$\frac{π}{2}$,0],且(α-$\frac{π}{2}$)3-sinα-2=0,8β3+2cos2β+1=0,则sin($\frac{α}{2}$+β)的值为( )
| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
1.已知函数f(x)=ax+elnx与g(x)=$\frac{{x}^{2}}{x-elnx}$的图象有三个不同的公共点,其中e为自然对数的底数,则实数a的取值范围为( )
| A. | a<-e | B. | a>1 | C. | a>e | D. | a<-3或a>1 |
5.已知函数y=f(x)(x∈R)的图象如图所示,则不等式x•f(x)<0的解集为( )
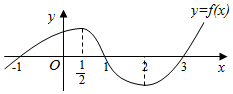

| A. | $(-∞,\frac{1}{2})∪(\frac{1}{2},2)$ | B. | (-1,0)∪(1,3) | C. | $(-∞,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(-∞,\frac{1}{2})∪(2,+∞)$ |
16.已知等比数列{an}中,a1•a9=64,a3+a7=20,则a35=( )
| A. | 49 | B. | $\frac{1}{{4}^{6}}$ | C. | $\frac{1}{{4}^{6}}$或49 | D. | -49 |
17.已知圆O的方程为 x2+y2=9,若抛物线C过点A(-1,0),B(1,0),且以圆O的切线为准线,则抛物线C的焦点F的轨迹方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(x≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(y≠0) | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(y≠0) |