题目内容
17.已知圆O的方程为 x2+y2=9,若抛物线C过点A(-1,0),B(1,0),且以圆O的切线为准线,则抛物线C的焦点F的轨迹方程为( )| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(x≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(y≠0) | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(y≠0) |
分析 设抛物线C的焦点为F(x,y),准线为l,过点A,B,O分别作AA′⊥l,BB′⊥l,OP⊥l,其中A′,B′,P分别为垂足,则l为圆的切线,P为切点,通过|FA|+|FB|=|AA′|+|BB′|=6>|AB|=2,说明点F的轨迹是以A,B为焦点的椭圆,求出焦点F的轨迹方程.
解答 解:设抛物线C的焦点为F(x,y),准线为l,
过点A,B,O分别作AA′⊥l,BB′⊥l,OP⊥l,
其中A′,B′,P分别为垂足,则l为圆的切线,P为切点,且|AA′|+BB′||=2|OP|=6.
因为抛物线过点A,B,所以|AA′|=|FA|,|FB|=|BB′|,
所以|FA|+|FB|=|AA′|+|BB′|=6>|AB|=2,
所以点F的轨迹是以A,B为焦点的椭圆,
且点F不在x轴上,所以抛物线C的焦点F的轨迹方程为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$(y≠0),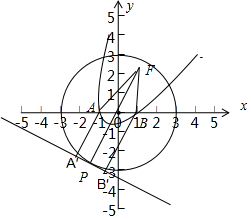
故选:D.
点评 本题主要考查了抛物线的定义与椭圆的标准方程,考查了学生数形结合的思想及计算能力.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
8.如果一个函数f(x)满足:(1)定义域为R;(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0;(3)任意x∈R,若t>0,总有f(x+t)>f(x),则f(x)可以是( )
| A. | y=-x | B. | y=3x | C. | y=x3 | D. | y=log3x |
12.设i是虚数单位,复数$\frac{a+2i}{1+i}$为实数,则实数a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥PF2,则以F1,F2为焦点且经过P的椭圆的离心率等于( )
| A. | .$\frac{{\sqrt{5}}}{5}$ | B. | .$\frac{{\sqrt{6}}}{3}$ | C. | .$\frac{{\sqrt{2}}}{2}$ | D. | .$\frac{1}{2}$ |