题目内容
5.已知函数y=f(x)(x∈R)的图象如图所示,则不等式x•f(x)<0的解集为( )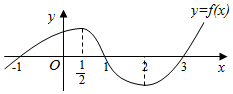
| A. | $(-∞,\frac{1}{2})∪(\frac{1}{2},2)$ | B. | (-1,0)∪(1,3) | C. | $(-∞,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(-∞,\frac{1}{2})∪(2,+∞)$ |
分析 利用函数的图象,结合不等式求解即可.
解答 解:由题意可知:x<0时,f(x)>0,此时x•f(x)<0,可得x∈(-1,0);
x>0时,f(x)<0,此时x•f(x)<0,可得x∈(1,3);
则不等式x•f(x)<0的解集为:(-1,0)∪(1,3).
故选:B.
点评 本题考查函数的图象的应用,考查数形结合思想的应用.

练习册系列答案
相关题目
16.若α是第三象限角,则下列各式中不成立的是( )
| A. | sin α+cos α<0 | B. | tan α-sin α<0 | C. | cos α-tan α<0 | D. | tan αsin α<0 |
17.若直线y=kx+3与圆(x-1)2+(y-2)2=4相加于M,N两点,且$|MN|≥2\sqrt{3}$,则k的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
12.设i是虚数单位,复数$\frac{a+2i}{1+i}$为实数,则实数a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |