题目内容
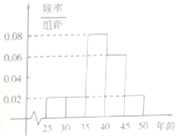 2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.
2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 25 | a | b |
(Ⅱ)现要从年龄较小的前3组中用分层抽样的方法抽取6人,则年龄在地1,2,3组的人数分别是多少?
(Ⅲ)在(Ⅱ)条件下,从这6人中随机抽取2人参加社区宣传交流活动,用列举法求恰有1人在第3组的频率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据小矩形的高=
,故频数比等于高之比,由此可得a、b的值,从而可确定N;
(Ⅱ)计算分层抽样的抽取比例为
=
,用抽取比例乘以每组的频数,可得每组抽取人数;
(Ⅲ)利用列举法写出从6人中随机抽取2人的所有基本事件,分别计算总个数与恰有1人在第3组的个数,根据古典概型概率公式计算.
| 频率 |
| 组距 |
(Ⅱ)计算分层抽样的抽取比例为
| 6 |
| 150 |
| 1 |
| 25 |
(Ⅲ)利用列举法写出从6人中随机抽取2人的所有基本事件,分别计算总个数与恰有1人在第3组的个数,根据古典概型概率公式计算.
解答:
解:(Ⅰ)由频率分布直方图可知,[25,30)与[30,35)两组的人数相同,
∴a=25人.
且b=25×
=100人.
总人数N=
=250人.
(Ⅱ)因为第1,2,3组共有25+25+100=150人,利用分层抽样在150名员工中抽取6人,每组抽取的人数分别为:
第1组的人数为6×
=1,
第2组的人数为6×
=1,
第3组的人数为6×
=4,
∴第1,2,3组分别抽取1人,1人,4人.
(Ⅲ)由(Ⅱ)可设第1组的1人为A,第2组的1人为B,
第3组的4人分别为C1,C2,C3,C4,
则从6人中抽取2人的所有可能结果为:
(A,B),(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),(B,C4),(C1,C2),(C1,C3),(C1,C4),(C2,C3),(C2,C4),(C3,C4),共有15种.
其中恰有1人年龄在第3组的所有结果为:(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),(B,C4),共有8种.
所以恰有1人年龄在第3组的概率为
.
∴a=25人.
且b=25×
| 0.08 |
| 0.02 |
总人数N=
| 25 |
| 0.02×5 |
(Ⅱ)因为第1,2,3组共有25+25+100=150人,利用分层抽样在150名员工中抽取6人,每组抽取的人数分别为:
第1组的人数为6×
| 25 |
| 125 |
第2组的人数为6×
| 25 |
| 125 |
第3组的人数为6×
| 100 |
| 125 |
∴第1,2,3组分别抽取1人,1人,4人.
(Ⅲ)由(Ⅱ)可设第1组的1人为A,第2组的1人为B,
第3组的4人分别为C1,C2,C3,C4,
则从6人中抽取2人的所有可能结果为:
(A,B),(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),(B,C4),(C1,C2),(C1,C3),(C1,C4),(C2,C3),(C2,C4),(C3,C4),共有15种.
其中恰有1人年龄在第3组的所有结果为:(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),(B,C4),共有8种.
所以恰有1人年龄在第3组的概率为
| 8 |
| 15 |
点评:本题考查了频率分布直方图及古典概型的概率计算,解答此类题的关键是读懂频率分布直方图的数据含义,属于中档题.

练习册系列答案
相关题目
点P在曲线y=
x3-
x+
上移动,设动点P处的切线的倾斜角为α,则α的取值范围是( )
| 1 |
| 3 |
| ||
| 3 |
| 3 |
| 4 |
| A、[0,π] | ||||||
B、(0,
| ||||||
C、[0,
| ||||||
D、[0,
|

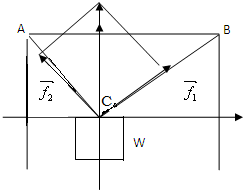 物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.
物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.