题目内容
已知tanα=2，计算：
（Ⅰ）
（Ⅱ）sin2α+sinαcosα-2cos2α
（Ⅰ）
| 2sinα-cosα |
| sinα+2cosα |
（Ⅱ）sin2α+sinαcosα-2cos2α
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（Ⅰ）原式分子分母除以cosα，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值；
（Ⅱ）原式分母看做“1”，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值．
（Ⅱ）原式分母看做“1”，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值．
解答：
解：（Ⅰ）∵tanα=2，
∴原式=
=
=
；
（Ⅱ）∵tanα=2，
∴原式=
=
=
=
．
∴原式=
| 2tanα-1 |
| tanα+2 |
| 2×2-1 |
| 2+2 |
| 3 |
| 4 |
（Ⅱ）∵tanα=2，
∴原式=
| sin2α+sinαcosα-2cos2α |
| sin2α+cos2α |
| tan2α+tanα-2 |
| tan2α+1 |
| 4+2-2 |
| 4+1 |
| 4 |
| 5 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知角α的终边过点P（
，-
），则sinα的值为（ ）
| 1 |
| 3 |
2
| ||
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=f（x）在点（2，1）处的切线与直线3x-y-2=0平行，则y′|x=2等于（ ）
| A、-3 | B、-1 | C、3 | D、1 |
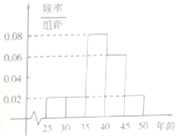2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险，建立全国统一的城乡居民基本养老保险制度，某街道社区N名居民接受当地电视台就该项制度的采访，他们的年龄在25随至50岁之间．按年龄分5组：[25，30），[30，35），[35，40），[40，45），[45，50]，得到的频率分布直方图如图所示，如表是年龄的频数分布表．
已知如图所示的流程图（未完成），设当箭头a指向①时输出的结果S=m，当箭头a指向②时，输出的结果S=n，求m+n的值．