题目内容
点P在曲线y=
x3-
x+
上移动，设动点P处的切线的倾斜角为α，则α的取值范围是（ ）
| 1 |
| 3 |
| ||
| 3 |
| 3 |
| 4 |
| A、[0，π] | ||||||
B、（0，
| ||||||
C、[0，
| ||||||
D、[0，
|
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求导数，利用斜率与倾斜角之间的关系，即可求出α的取值范围．
解答：
解：∵y=
x3-
x+
，
∴y′=x2-
≥-
，
∴tanα≥-
，
∵α∈[0，π），
∴α的取值范围是[0，
）∪[
，π）．
故选：D．
| 1 |
| 3 |
| ||
| 3 |
| 3 |
| 4 |
∴y′=x2-
| ||
| 3 |
| ||
| 3 |
∴tanα≥-
| ||
| 3 |
∵α∈[0，π），
∴α的取值范围是[0，
| π |
| 2 |
| 5π |
| 6 |
故选：D．
点评：本题考查导数的几何意义，考查斜率与倾斜角之间的关系，正确理解导数的几何意义是关键．
练习册系列答案
相关题目
已知函数f（x）是R上的偶函数，若对于x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=log2（x+1），则当x∈（-∞，+∞）时，f（-2011）+f（2012）的值为（ ）
| A、-2 | B、-1 | C、1 | D、2 |
△ABC中，若a=1，c=2，B=30°，则△ABC的面积为（ ）
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知角α的终边过点P（
，-
），则sinα的值为（ ）
| 1 |
| 3 |
2
| ||
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=f（x）是定义在R上的奇函数，且当x＞0时，f（x）+xf′（x）＞0．（其中f′（x）是f（x）的导函数）．设a=（log
4）•f（log
4），b=
•f（
）．c=（lg
）•f（lg
），判断大小为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| A、c＞a＞b |
| B、a＞b＞c |
| C、c＞b＞a |
| D、a＞c＞b |
甲、乙两名考生在填报志愿时都选中了A、B、C、D四所需要面试的院校，这四所院校的面试安排在同一时间，因此甲、乙都只能在这四所院校中选择一所做志愿，假设每位同学选择各个院校是等可能的，则甲、乙选择同一所院校的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
某学校组织的数学竞赛中，学生的竞赛成绩ξ-N（100，σ2），P（ξ＞120）=a，P（80＜ξ≤100）=b，则直线ax+by+
=0与圆x2+y2=2的位置关系是（ ）
| 1 |
| 2 |
| A、相离 | B、相交 |
| C、相离或相切 | D、相交或相切 |
已知函数y=f（x）在点（2，1）处的切线与直线3x-y-2=0平行，则y′|x=2等于（ ）
| A、-3 | B、-1 | C、3 | D、1 |
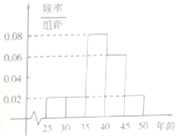2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险，建立全国统一的城乡居民基本养老保险制度，某街道社区N名居民接受当地电视台就该项制度的采访，他们的年龄在25随至50岁之间．按年龄分5组：[25，30），[30，35），[35，40），[40，45），[45，50]，得到的频率分布直方图如图所示，如表是年龄的频数分布表．