题目内容
已知α是第四象限角，则
必定不在第 象限．
| α |
| 3 |
考点：象限角、轴线角
专题：三角函数的求值
分析：先根据α所在的象限，判断出α的范围，进而分别求得
的范围，进而确定答案．
| α |
| 3 |
解答：
解：∵α在第四象限，
∴α∈（2kπ+
，2kπ+2π）
∴
∈（
kπ+
，
kπ+
），
当k=3n+1时
∈(2kπ+
，2kπ+
)为第三象限，
当k=3n+2时，
∈(2kπ+
，2kπ+2π)在第四象限，
当k=3n+3时，
∈(2kπ+
，2kπ+
π)在第二象限，
则
必定不在第一象限．
故答案为：一．
∴α∈（2kπ+
| 3π |
| 2 |
∴
| α |
| 3 |
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3 |
| 2π |
| 3 |
当k=3n+1时
| α |
| 3 |
| 7π |
| 6 |
| 4π |
| 3 |
当k=3n+2时，
| α |
| 3 |
| 11π |
| 6 |
当k=3n+3时，
| α |
| 3 |
| 5π |
| 2 |
| 8 |
| 3 |
则
| α |
| 3 |
故答案为：一．
点评：本题主要考查了半角的三角函数和象限角的问题．解题的关键是根据角的范围确定角所在的象限．
练习册系列答案
相关题目
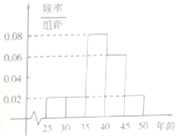2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险，建立全国统一的城乡居民基本养老保险制度，某街道社区N名居民接受当地电视台就该项制度的采访，他们的年龄在25随至50岁之间．按年龄分5组：[25，30），[30，35），[35，40），[40，45），[45，50]，得到的频率分布直方图如图所示，如表是年龄的频数分布表．
已知如图所示的流程图（未完成），设当箭头a指向①时输出的结果S=m，当箭头a指向②时，输出的结果S=n，求m+n的值．
运行如图所示的程序框图，若输出的结果是7，则判断框中的横线上可以填入的最大整数为（ ）| A、7 | B、8 | C、9 | D、10 |