题目内容
已知等差数列{an}的前n项和为Sn,且a2+a7+a12=-6,S20=-110.
(1)求数列{an}的通项an;
(2)若等比数列{bn}的前n项和为Tn,b1=4,公比q=-
,且对任意的m,n∈N*,都有Sn<Tm+t,求实数t的取值范围.
(1)求数列{an}的通项an;
(2)若等比数列{bn}的前n项和为Tn,b1=4,公比q=-
| 1 |
| 2 |
考点:数列的求和,等差数列的性质
专题:综合题
分析:(1)由已知列出方程组
,求出
代入等差数列的通项公式即可;
(2)求出等差数列{an}的前n项和为Sn及等比数列{bn}的前n项和为Tn,将对任意的m,n∈N*,都有Sn<Tm+t,转化为求Sn-Tm,求的最大值.
|
|
(2)求出等差数列{an}的前n项和为Sn及等比数列{bn}的前n项和为Tn,将对任意的m,n∈N*,都有Sn<Tm+t,转化为求Sn-Tm,求的最大值.
解答:
解:(1)∵a2+a7+a12=-6,S20=-110.
∴
,
解得
∴an=a1+(n-1)d=-n+5.
(2)由(1)知Sn= a1n+
d=-
+
n,
∵等比数列{bn}中b1=4,公比q=-
,
∴Tm=
=
[1-(-
)m],
∵任意的m,n∈N*,都有Sn<Tm+t,
(-
+
n)-
[1-(-
)m]<t对任意的m,n∈N*,都成立
当n=4或5时,Sn最大为10;
当m=2时Tm最小为2;
∴当n=4或5且m=2时(-
+
n)-
[1-(-
)m]最大为10-2=8,
∴t>8.
∴
|
解得
|
∴an=a1+(n-1)d=-n+5.
(2)由(1)知Sn= a1n+
| n(n-1) |
| 2 |
| n2 |
| 2 |
| 9 |
| 2 |
∵等比数列{bn}中b1=4,公比q=-
| 1 |
| 2 |
∴Tm=
4[1-(-
| ||
1+
|
| 8 |
| 3 |
| 1 |
| 2 |
∵任意的m,n∈N*,都有Sn<Tm+t,
(-
| n2 |
| 2 |
| 9 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
当n=4或5时,Sn最大为10;
当m=2时Tm最小为2;
∴当n=4或5且m=2时(-
| n2 |
| 2 |
| 9 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
∴t>8.
点评:本题考查等差数列、等比数列的通项公式,前n项和公式;不等式恒成立问题,是一道综合题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
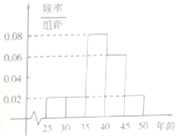 2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.
2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.