题目内容
已知函数f（x）=
，且f（x）在x=2处取得极值．
（1）求f（x）在x=2处的切线方程；
（2）求f（x）在[0，3]上的最大值及最小值．
| x-a |
| ex |
（1）求f（x）在x=2处的切线方程；
（2）求f（x）在[0，3]上的最大值及最小值．
考点：利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题：计算题,导数的综合应用
分析：（1）由题意求导f′（x）=
，令f′（2）=0可解出a，再求f（x）在x=2处的切线方程；
（2）由（1）易知f（x）在[0，2]上单调递增，在[2，3]上单调递减，从而求f（x）在[0，3]上的最大值及最小值．
| 1+a-x |
| ex |
（2）由（1）易知f（x）在[0，2]上单调递增，在[2，3]上单调递减，从而求f（x）在[0，3]上的最大值及最小值．
解答：
解：（1）f′（x）=
，
由题意可得，f′（2）=0，
从而解得，a=1，
故f（x）=
，
则f（2）=
，
故f（x）在x=2处的切线方程为y=
；
（2）由（1）知，f（x）=
，f′（x）=
，
故f（x）在[0，2]上单调递增，在[2，3]上单调递减，
又∵f（0）=-1，f（2）=
，f（3）=
，
故f（x）在[0，3]上的最大值为
，
最小值为-1．
| 1+a-x |
| ex |
由题意可得，f′（2）=0，
从而解得，a=1，
故f（x）=
| x-1 |
| ex |
则f（2）=
| 1 |
| e2 |
故f（x）在x=2处的切线方程为y=
| 1 |
| e2 |
（2）由（1）知，f（x）=
| x-1 |
| ex |
| 2-x |
| ex |
故f（x）在[0，2]上单调递增，在[2，3]上单调递减，
又∵f（0）=-1，f（2）=
| 1 |
| e2 |
| 2 |
| e3 |
故f（x）在[0，3]上的最大值为
| 1 |
| e2 |
最小值为-1．
点评：本题考查了导数的综合应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知i是虚数单位，若复数Z=a+bi（a，b∈R）在复平面内对应的点位于第四象限，则复数Z•i在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知sin（π+α）=
，且α是第四象限角，则cos（α-2π）的值是（ ）
| 2 |
| 3 |
A、±
| ||||
B、
| ||||
C、±
| ||||
D、
|
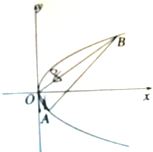如图，已知抛物线有一个内接直角三角形，直角顶点在原点，两直角边分别为1和8，求抛物线方程．