题目内容
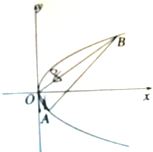 如图,已知抛物线有一个内接直角三角形,直角顶点在原点,两直角边分别为1和8,求抛物线方程.
如图,已知抛物线有一个内接直角三角形,直角顶点在原点,两直角边分别为1和8,求抛物线方程.考点:抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:依题意,设直线OA的方程为y=kx(k≠0),则直线OB的方程为y=-
x,分别联立直线与抛物线方程y2=2px,可求得A、B两点的坐标,利用,|OA|=1,|OB|=8,即可求得k与p的值,从而可得抛物线方程.
| 1 |
| k |
解答:
 解:设直线OA的方程为y=kx(k≠0),则直线OB的方程为y=-
解:设直线OA的方程为y=kx(k≠0),则直线OB的方程为y=-
x,由
得:x=0或x=
,
∴A(
,
),同理可得B(2pk2,-2pk),
由图知,|OA|=1,|OB|=8,
∴(
-0)2+(
-0)2=1,即4p2•
=1①,
(2pk2-0)2+(-2pk-0)2=64,即4p2•k2(k2+1)=64②,
得:k6=64,k2=4,代入①得:p2=
,又p>0,
∴p=
.
∴抛物线方程为:y2=
x.
 解:设直线OA的方程为y=kx(k≠0),则直线OB的方程为y=-
解:设直线OA的方程为y=kx(k≠0),则直线OB的方程为y=-| 1 |
| k |
|
| 2p |
| k2 |
∴A(
| 2p |
| k2 |
| 2p |
| k |
由图知,|OA|=1,|OB|=8,
∴(
| 2p |
| k2 |
| 2p |
| k |
| k2+1 |
| k4 |
(2pk2-0)2+(-2pk-0)2=64,即4p2•k2(k2+1)=64②,
| ② |
| ① |
| 4 |
| 5 |
∴p=
2
| ||
| 5 |
∴抛物线方程为:y2=
4
| ||
| 5 |
点评:本题考查抛物线的标准方程,着重考查两点间的距离公式的应用,考查方程思想与运算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=x2+2x,若存在实数a,b(0<a<b),使f(x)在[a,b]上的值域是[
,
].则b-a的最小值是( )
| 1 |
| b |
| 1 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|