题目内容
已知直线m、n,平面α、β,给出下列命题:其中正确的命题是( )
①若m⊥α,n⊥β,且m⊥n,则α⊥β
②若m∥α,n∥β,且m∥n,则α∥β
③若m⊥α,n∥β,且m⊥n,则α⊥β
④若m⊥α,n∥β,且m∥n,则α⊥β
①若m⊥α,n⊥β,且m⊥n,则α⊥β
②若m∥α,n∥β,且m∥n,则α∥β
③若m⊥α,n∥β,且m⊥n,则α⊥β
④若m⊥α,n∥β,且m∥n,则α⊥β
| A、①③ | B、②④ | C、③④ | D、①④ |
考点:命题的真假判断与应用,直线与平面垂直的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:①利用面面垂直的判定定理即可判断出;
②利用线线、线面平行的判定与性质即可得出;
③利用线面平行于垂直的判定与性质定理即可得出;
④利用面面垂直的判定定理即可得出.
②利用线线、线面平行的判定与性质即可得出;
③利用线面平行于垂直的判定与性质定理即可得出;
④利用面面垂直的判定定理即可得出.
解答:
解:①若m⊥α,n⊥β,且m⊥n,利用面面垂直的判定定理可得α⊥β,因此正确;
②若m∥α,n∥β,且m∥n,则α∥β或相交,因此不正确;
③若m⊥α,n∥β,且m⊥n,则α∥β,因此不正确;
④若m⊥α,n∥β,且m∥n,利用面面垂直的判定定理可得α⊥β,因此正确.
综上可知:只有①④正确.
故选:D.
②若m∥α,n∥β,且m∥n,则α∥β或相交,因此不正确;
③若m⊥α,n∥β,且m⊥n,则α∥β,因此不正确;
④若m⊥α,n∥β,且m∥n,利用面面垂直的判定定理可得α⊥β,因此正确.
综上可知:只有①④正确.
故选:D.
点评:本题考查了线线、线面与面面平行与垂直的判定与性质定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知O为坐标原点,P1、P2是双曲线
-
=1上的点.P是线段P1P2的中点,直线OP、P1P2的斜率分别为k1、k2,若2≤k1≤4,则k2的取值范围是( )
| x2 |
| 9 |
| y2 |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知x,y满足约束条件
,则目标函数z=2x-3y的最大值( )
|
| A、2 | B、3 | C、4 | D、5 |
集合A={x|1<x<3},B={x|x≤2},则A∩B=( )
| A、{x|x<3} |
| B、{x|2≤x<3} |
| C、{x|1<x≤2} |
| D、{x|1<x<2} |
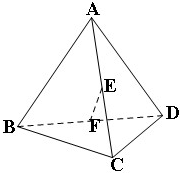 如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是
如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是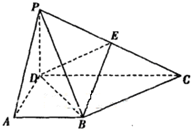 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.