题目内容
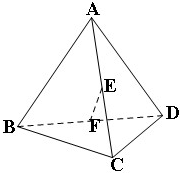 如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是
如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是①EF∥AB;
②当二面角A-BD-C的大小为60°时,AC=2;
③当四面体ABCD的体积最大时,AC=
| 6 |
④AC垂直于截面BDE.
考点:命题的真假判断与应用,棱柱、棱锥、棱台的体积,直线与平面垂直的性质,二面角的平面角及求法
专题:综合题,空间位置关系与距离
分析:①取AD的中点P,易知PF∥AB,利用反证法可知EF不与AB平行;
②依题意知,△AFC为边长为
的等边三角形,从而可知②的正误;
③经分析知,当平面ABC⊥平面BCD时,四面体ABCD的体积最大,此时△AFC为边长为
的等腰直角三角形,从而可求其斜边AC的长;
④利用线面垂直的判定定理,可证得AC垂直于截面BDE,从而可知④之正误.
②依题意知,△AFC为边长为
| 3 |
③经分析知,当平面ABC⊥平面BCD时,四面体ABCD的体积最大,此时△AFC为边长为
| 3 |
④利用线面垂直的判定定理,可证得AC垂直于截面BDE,从而可知④之正误.
解答:
解:依题意,作图如下:

①,F为BD的中点,取AD的中点P,易知PF∥AB,若EF∥AB,则EF∥PF,与二者相交矛盾,故EF不与AB平行,①错误;
②,△ABD与△BCD均为边长为2的等边三角形,连接AF,CF,则AF⊥BD,CF⊥BD,∠AFC就是二面角A-BD-C的平面角,
若∠AFC=60°,则△AFC为等边三角形,AC=AF=ABsin60°=2×
=
,故②错误;
③,当四面体ABCD以平面BCD为底面,高最大时,
该四面体ABCD的体积最大,此时平面ABC⊥平面BCD,AF就是其高,其值为
,
又此时△AFC为边长为
的等腰直角三角形,故AC=
•
=
,故③正确;
④,∵AF=FC,△AFC为等腰三角形,E为AC的中点,
∴AC⊥EF,又AC⊥BD,EF∩BD=F,
∴AC垂直于截面BDE,即④正确;
综上所述,命题中正确的是:③④.
故答案为:③④.

①,F为BD的中点,取AD的中点P,易知PF∥AB,若EF∥AB,则EF∥PF,与二者相交矛盾,故EF不与AB平行,①错误;
②,△ABD与△BCD均为边长为2的等边三角形,连接AF,CF,则AF⊥BD,CF⊥BD,∠AFC就是二面角A-BD-C的平面角,
若∠AFC=60°,则△AFC为等边三角形,AC=AF=ABsin60°=2×
| ||
| 2 |
| 3 |
③,当四面体ABCD以平面BCD为底面,高最大时,
该四面体ABCD的体积最大,此时平面ABC⊥平面BCD,AF就是其高,其值为
| 3 |
又此时△AFC为边长为
| 3 |
| 2 |
| 3 |
| 6 |
④,∵AF=FC,△AFC为等腰三角形,E为AC的中点,
∴AC⊥EF,又AC⊥BD,EF∩BD=F,
∴AC垂直于截面BDE,即④正确;
综上所述,命题中正确的是:③④.
故答案为:③④.
点评:本题考查命题的真假判断与应用,考查二面角的平面角及其应用,考查作图、分析与综合运算能力,属于难题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 给出下列三个命题:
给出下列三个命题: