题目内容
8.将圆x2+y2=1上每一点的纵坐标不变,横坐标变为原来的$\frac{1}{3}$,得曲线C.(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l:3x+y+1=0与C的交点为P1、P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
分析 (Ⅰ)由坐标变换公式得x=3x′,y=y′,代入x2+y2=1中,得9x'2+y'2=1,由此能求出曲线C的参数方程.
(Ⅱ)联立$\left\{\begin{array}{l}{9{x}^{2}+{y}^{2}=1}\\{3x+y=1}\end{array}\right.$,得P1(-$\frac{1}{3}$,0),P2(0,-1),由此能求出过线段P1P2的中点且与l垂直的直线的极坐标方程.
解答 解:(Ⅰ)∵将圆x2+y2=1上每一点的纵坐标不变,横坐标变为原来的$\frac{1}{3}$,得曲线C.
∴由坐标变换公式$\left\{\begin{array}{l}{{x}^{'}=\frac{1}{3}x}\\{{y}^{'}=y}\end{array}\right.$,得x=3x′,y=y′,
代入x2+y2=1中,得9x'2+y'2=1,
故曲线C的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{3}cosθ}\\{y=sinθ}\end{array}\right.$( θ为参数).(5分)
(Ⅱ)联立$\left\{\begin{array}{l}{9{x}^{2}+{y}^{2}=1}\\{3x+y=-1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-\frac{1}{3}}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
由题知,P1(-$\frac{1}{3}$,0),P2(0,-1),P1 P2线段中点M(-$\frac{1}{6}$,-$\frac{1}{2}$),
${k}_{{P}_{1}{P}_{2}}$=$\frac{-1-0}{0+\frac{1}{3}}$=-3,故P1 P2线段中垂线的方程为y+$\frac{1}{2}$=$\frac{1}{3}$(x+$\frac{1}{6}$),(8分)
即3x-9y-4=0,即极坐标方程为3ρcosθ-9ρsinθ-4=0.(10分)
点评 本题考查曲线的参数方程的求法,考查过线段的中点且与直线垂直的直线的极坐标方程的求法,是中档题,解题时要认真审题,注意参数方程、直角坐标方程、极坐标方程互化公式的合理运用.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案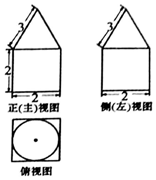
| A. | 4+2$\sqrt{2}$π | B. | 8+2$\sqrt{2}$π | C. | 4+$\frac{2\sqrt{2}}{3}$π | D. | 8+$\frac{2\sqrt{2}}{3}$π |
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |