��Ŀ����
3����ֱ������ϵ�У���ԭ��Ϊ���㣬x��Ǹ�����Ϊ���Ὠ��������ϵ��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$��tΪ������������C�ļ����귽��Ϊ��=6cos����1����l�IJ��������е�t=$\sqrt{2}$ʱ���õ�M�㣬��M�ļ����������C��ֱ�����귽�̣�
��2������P��1��1����l������C����A��B���㣬��$\frac{1}{|PA|}+\frac{1}{|PB|}$��
���� ��1��t=$\sqrt{2}$����ֱ��l�IJ����������M��0��2�����Ӷ������M�ļ����꣬������C�ļ����귽�����������C��ֱ�����귽�̣�
��2������ֱ��l�IJ������̺�����C��ֱ�����귽�̵�${t}^{2}+3\sqrt{2}t-4=0$���ɴ�����Τ�ﶨ�������$\frac{1}{|PA|}+\frac{1}{|PB|}$��ֵ��
��� �⣺��1����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$��tΪ��������
l�IJ��������е�t=$\sqrt{2}$ʱ���õ�M�㣬
���M��ֱ������ΪM��0��2����
��$��=\sqrt{0+4}=2$��$��=\frac{��}{2}$�����M�ļ�����ΪM��2��$\frac{��}{2}$����
������C�ļ����귽��Ϊ��=6cos�ȣ�����2=6��cos�ȣ�
������C��ֱ�����귽��Ϊx2-6x+y2=0��
��2������ֱ��l�IJ������̺�����C��ֱ�����귽�̵ã�
${t}^{2}+3\sqrt{2}t-4=0$��
��$\left\{\begin{array}{l}{{t}_{1}+{t}_{2}=-3\sqrt{2}}\\{{t}_{1}{t}_{2}=-4��0}\end{array}\right.$��
��$\frac{1}{|PA|}+\frac{1}{|PB|}$=$\frac{1}{|{t}_{1}|}+\frac{1}{|{t}_{2}|}$=$\frac{|{t}_{1}|+|{t}_{2}|}{|{t}_{1}{t}_{2}|}$
=$\frac{|{t}_{1}-{t}_{2}|}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{34}}{4}$��
���� ���⿼���ļ���������ߵļ����귽�̵��������ҳ��������е��⣬����ʱҪ�������⣬ע��������̡�ֱ�����귽�̡������귽�̻�����ʽ�ĺ������ã�

| A�� | ��$\frac{��}{3}$��0�� | B�� | �� $\frac{��}{4}$��0�� | C�� | ��-$\frac{��}{12}$��0�� | D�� | ��$\frac{��}{2}$��0�� |
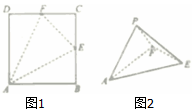 ��ͼ1��ABCD�DZ߳�Ϊ2�������Σ���E��F�ֱ�ΪBC��CD���е㣬����ABE����ECF����FDA�ֱ���AE��EF��FA����ʹB��C��D�����غ��ڵ�P����������PAEF���ĸ�������ͬһ�������ϣ������ı�����ǣ�������
��ͼ1��ABCD�DZ߳�Ϊ2�������Σ���E��F�ֱ�ΪBC��CD���е㣬����ABE����ECF����FDA�ֱ���AE��EF��FA����ʹB��C��D�����غ��ڵ�P����������PAEF���ĸ�������ͬһ�������ϣ������ı�����ǣ�������| A�� | $\sqrt{6}��$ | B�� | 6�� | C�� | $4\sqrt{3}��$ | D�� | 12�� |
| A�� | ��0��2�� | B�� | ��-2��0�� | C�� | {1��2} | D�� | {1} |
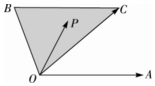 ��֪ͼ�С�AOC+2��BOC=�У�|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|��BC��OA��PΪͼ�е���Ӱ�У����߽磩����㣬����$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$��������ȷ���Ǣ٢ۢ�
��֪ͼ�С�AOC+2��BOC=�У�|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|��BC��OA��PΪͼ�е���Ӱ�У����߽磩����㣬����$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$��������ȷ���Ǣ٢ۢ� ��ͼ����֪����A-OCB�У�AO�͵���BOC���ҡ�BAO=��CAO=$\frac{��}{6}$��AB=4����DΪ�߶�AB���е㣬�Ƕ����B-AO-C�Ĵ�СΪ�ȣ�
��ͼ����֪����A-OCB�У�AO�͵���BOC���ҡ�BAO=��CAO=$\frac{��}{6}$��AB=4����DΪ�߶�AB���е㣬�Ƕ����B-AO-C�Ĵ�СΪ�ȣ�