题目内容
17.在△ABC中,“A<B<C”是“cos2A>cos2B>cos2C”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 在△ABC中,“A<B<C”?a<b<c,再利用正弦定理、同角三角函数基本关系式、倍角公式即可得出.
解答 解:在△ABC中,“A<B<C”?a<b<c?sinA<sinB<sinC?sin2A<sin2B<sin2C
?1-2sin2A>1-2sin2B>1-2sin2C?“cos2A>cos2B>cos2C”.
∴在△ABC中,“A<B<C”是“cos2A>cos2B>cos2C”的充要条件.
故选:C.
点评 本题考查了正弦定理、同角三角函数基本关系式、倍角公式、不等式的性质、三角形三边大小关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.已知集合M={x∈Z|-x2+3x>0},N={x|x2-4<0},则M∩N=( )
| A. | (0,2) | B. | (-2,0) | C. | {1,2} | D. | {1} |
9.已知复数z=$\frac{i}{1+i}$,其中i为虚数单位,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
16.设向量$\overrightarrow a=(1,3)$,$\overrightarrow b=(-2,m)$,若$\overrightarrow a$与$\overrightarrow a+\overrightarrow b$垂直,则m的值为( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{8}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{8}{3}$ |
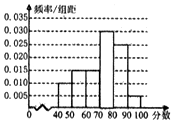 某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.