题目内容
19.在正方体A1B1C1D1-ABCD中,给出以下命题:①平面A1BD∥平面D1B1C;
②存在无数条直线,它与该正方体的六个表面所在平面所成的角都相等;
③不存在平面,与该正方体的六个表面所在平面所成的锐二面角的大小都相等;
④AD1与平面A1BD所成角的正弦值为$\frac{{\sqrt{6}}}{3}$.
其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,依据面面平行的判定可判定;
②过点A与三个平面AB′,AC,AD′所成角都相等的直线分有4条,所有与之平行的直线都满足条件,存在无数条直线,
③,面A1C1B与过定点B1的侧面所成角相等,与六个侧面所成角一定等
④如图连结AD1交A1D于E,连结AC1交面A1BD于O,
易知AC1⊥面A1BD,连结EO,故∠AEO就是AD1与平面A1BD所成角,sin∠AEO=$\frac{AO}{AE}=\frac{\sqrt{6}}{3}$,.
解答 解:对于①,如图所示∵DB∥D1B1,A1D∥B1C,由面面平行的判定可判定平面A1BD∥平面D1B1C,故正确;
对于②,过点A与三个平面AB′,AC,AD′所成角都相等的直线分两类:
第一类:通过点A位于三条棱之间的直线有一条体对角线AC1,第二类:在图形外部和每面所成角和另两个面所成角相等,有3条,合计4条,所有与之平行的直线都满足条件,存在无数条直线,故正确.
对于③,如图面A1C1B与过定点B1的侧面所成角相等,与六个侧面所成角一定等,故错;
对于④,如图连结AD1交A1D于E,连结AC1交面A1BD于O,
易知AC1⊥面A1BD,连结EO,故∠AEO就是AD1与平面A1BD所成角,sin∠AEO=$\frac{AO}{AE}=\frac{\sqrt{6}}{3}$,故正确.
故选:C.
点评 本题考查了空间线线、线面的位置关系,即线面角、面面角的求解,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.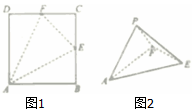 如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
 如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )| A. | $\sqrt{6}π$ | B. | 6π | C. | $4\sqrt{3}π$ | D. | 12π |
9.已知复数z=$\frac{i}{1+i}$,其中i为虚数单位,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
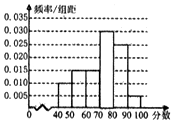 某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
某中学选取20名优秀同学参加2015年英语应用知识竞赛,将他们的成绩(百分制)(均为整数)分成6组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.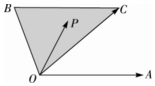 已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤
已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤