��Ŀ����
16����֪�ȱߡ�AB��C��߳�Ϊ$\sqrt{2}$����BCD�У�$BD=CD=1��BC=\sqrt{2}$����ͼ1��ʾ�����ֽ�B��B�䣬C��C���غϣ�����AB��C����������ʹ��$AD=\sqrt{3}$����ͼ2��ʾ����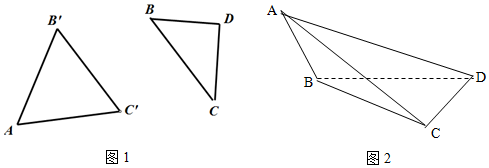
��1����BC���е�O����֤��ƽ��BCD��ƽ��AOD��
��2�����߶�AC���Ƿ����һ��E��ʹED����BCD��30��ǣ������ڣ����CE�ij��ȣ��������ڣ���˵�����ɣ�
��3��������A-BCD�������ı������
���� ��1������ƽ�漸���е��������ε����ߺ�һ��������洹ֱ���ж����������洹ֱ���ж����������ɵ�֤��
��2������1����AH��DO����DO���ӳ�����H������ƽ�漸�����й����ʣ��Լ����洹ֱ�����洹ֱ�����ʣ��ɵá�EDF����ED����BCD���ɵĽǣ�����ֱ�������ε�֪ʶ������ɵ�CE��
����2����DΪ����ԭ�㣬��ֱ��DB��DC�ֱ�Ϊx�ᣬy����������Թ�D��ƽ��BCD��ֱ��ֱ��Ϊz�ᣬ�����ռ�ֱ������ϵ����CE=x�����E�����꣬���÷��������Լ������ļнǹ�ʽ�����㼴�ɵõ�����
��3����ԭͼ���γ������壬��AC=$\sqrt{2}$���ɵ�������߳�Ϊ1���ɵ�������ֱ����Ϊ������ĶԽ��߳�������ı������ʽ�����㼴�ɵõ�����
��� 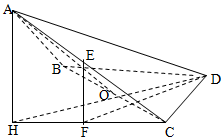 �⣺��1��֤�����ߡ�ABCΪ�ȱ������Σ���BCDΪ���������Σ�
�⣺��1��֤�����ߡ�ABCΪ�ȱ������Σ���BCDΪ���������Σ�
��OΪ�е㣬
��BC��AO��BC��DO��
��AO��DO=O����BC��ƽ��AOD��
��BC?��ABC
��ƽ��BCD��ƽ��AOD����3�֣�
��2������1����AH��DO����DO���ӳ�����H��
��ƽ��BCD��ƽ��AOD=HD����AH��ƽ��BCD��
��Rt��BCD��$OD=\frac{1}{2}BC=\frac{{\sqrt{2}}}{2}$��
��Rt��ACO��$AO=\frac{{\sqrt{3}}}{2}AC=\frac{{\sqrt{6}}}{2}$��
�ڡ�AOD�У�$cos��ADO=\frac{{A{D^2}+O{D^2}-A{O^2}}}{2AD•OD}=\frac{{\sqrt{6}}}{3}$��
��$sin��ADO=\frac{{\sqrt{3}}}{3}$����Rt��ADH��AH=ADsin��ADO=1��
��$CE=x��0��x��\sqrt{2}��$����EF��CH��F��ƽ��AHC��ƽ��BCD��
��EF��ƽ��BCD����EDF����ED����BCD���ɵĽǣ�
��$\frac{EF}{AH}=\frac{CE}{AC}$����$EF=\frac{{\sqrt{2}}}{2}x$��������
��Rt��CDE��$DE=\sqrt{C{E^2}+C{D^2}}=\sqrt{{x^2}+1}$��
ҪʹED����BCD��30��ǣ�ֻ��ʹ$\frac{{\frac{{\sqrt{2}}}{2}x}}{{\sqrt{{x^2}+1}}}=\frac{1}{2}$��
��x=1����CE=1ʱ��ED����BCD��30��ǡ���9�֣�
����2���ڽⷨ1�нӣ���������DΪ����ԭ�㣬
��ֱ��DB��DC�ֱ�Ϊx�ᣬy���������
�Թ�D��ƽ��BCD��ֱ��ֱ��Ϊz�ᣬ�����ռ�ֱ������ϵ
��$D��0��0��0����E��\frac{{\sqrt{2}}}{2}x��1��\frac{{\sqrt{2}}}{2}x��$��$\overrightarrow{DE}=��\frac{{\sqrt{2}}}{2}x��1��\frac{{\sqrt{2}}}{2}x��$��
��ƽ��BCD��һ��������Ϊ$\overrightarrow n=��0��0��1��$��ҪʹED����BCD��30��ǣ�
ֻ��ʹ$\overrightarrow{DE}��\overrightarrow n$��60�㣬
ֻ��ʹ$\frac{{|{\overrightarrow{DE}•\overrightarrow n}|}}{{|{\overrightarrow{DE}}|•|{\overrightarrow n}|}}=cos{60��}$����$\frac{{\frac{{\sqrt{2}}}{2}x}}{{\sqrt{{x^2}+1}}}=\frac{1}{2}$����x=1��
��CE=1ʱED����BCD��30��ǣ�
��3����ԭͼ���γ������壬��AC=$\sqrt{2}$���ɵ�������߳�Ϊ1��
��������ֱ��Ϊ$\sqrt{3}$�����뾶$r=\frac{{\sqrt{3}}}{2}$��
�������S=4��r2=3�С���12�֣�
���� ���⿼�����洹ֱ���ж���ע���������洹ֱ���ж�����������ǵ���ע����������ǵĶ���������������������������ı������ע�����ø˼�룬������������������������е��⣮

| A�� | ��a•3=b•3����a=b����Ƴ� ��a•0=b•0����a=b | |
| B�� | ����a+b��c=ac+bc����Ƴ� $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$��c��0�� | |
| C�� | ����a+b��c=ac+bc����Ƴ� ��a•b��c=ac•bc | |
| D�� | ����ab��n=anbn����Ƴ� ��a+b��n=an+bn |
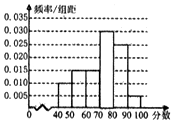 ij��ѧѡȡ20������ͬѧ�μ�2015��Ӣ��Ӧ��֪ʶ�����������ǵijɼ����ٷ��ƣ�����Ϊ�������ֳ�6��õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�����۲�ͼ���е���Ϣ���ش��������⣮
ij��ѧѡȡ20������ͬѧ�μ�2015��Ӣ��Ӧ��֪ʶ�����������ǵijɼ����ٷ��ƣ�����Ϊ�������ֳ�6��õ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�����۲�ͼ���е���Ϣ���ش��������⣮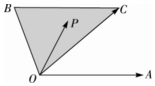 ��֪ͼ�С�AOC+2��BOC=�У�|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|��BC��OA��PΪͼ�е���Ӱ�У����߽磩����㣬����$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$��������ȷ���Ǣ٢ۢ�
��֪ͼ�С�AOC+2��BOC=�У�|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|��BC��OA��PΪͼ�е���Ӱ�У����߽磩����㣬����$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$��������ȷ���Ǣ٢ۢ�