题目内容
18．某几何体的三视图如图所示，则该几何体的体积为（ ）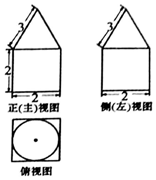
| A． | 4+2$\sqrt{2}$π | B． | 8+2$\sqrt{2}$π | C． | 4+$\frac{2\sqrt{2}}{3}$π | D． | 8+$\frac{2\sqrt{2}}{3}$π |
分析 该几何体由上下两部分组成的，上面是一个圆锥，下面是一个正方体．
解答 解：该几何体由上下两部分组成的，上面是一个圆锥，下面是一个正方体．
∴该几何体的体积V=${2}^{3}+\frac{1}{3}×π×{1}^{2}×2\sqrt{2}$=8+$\frac{2\sqrt{2}}{3}π$．
故选：D．
点评 本题考查了圆柱与圆锥的三视图、体积计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
优等生题库系列答案
相关题目
6．在以下的类比推理中结论正确的是（ ）
| A． | 若a•3=b•3，则a=b类比推出 若a•0=b•0，则a=b | |
| B． | 若（a+b）c=ac+bc类比推出 $\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$（c≠0） | |
| C． | 若（a+b）c=ac+bc类比推出 （a•b）c=ac•bc | |
| D． | 若（ab）n=anbn类比推出 （a+b）n=an+bn |
13．将函数f（x）=sin2x+$\sqrt{3}$cos2x图象上所有点向右平移$\frac{π}{6}$个单位长度，得到函数g （x）的图象，则g（x）图象的一个对称中心是（ ）
| A． | （$\frac{π}{3}$，0） | B． | （ $\frac{π}{4}$，0） | C． | （-$\frac{π}{12}$，0） | D． | （$\frac{π}{2}$，0） |
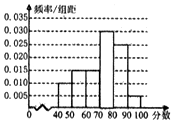某中学选取20名优秀同学参加2015年英语应用知识竞赛，将他们的成绩（百分制）（均为整数）分成6组后，得到频率分布直方图（如图），观察图形中的信息，回答下列问题．