题目内容
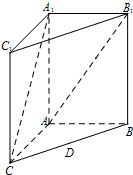 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)若点D是线段BC的中点,请问在线段AB1是否存在点E,使得DE∥面AA1C1C?若存在,请说明点E的位置,若不存在,请说明理由;
(Ⅲ)(本小问只理科学生做)求二面角C-A1B1-C1的大小.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)因为四边形AA1C1C为正方形,所以AA1⊥AC.因为平面ABC⊥平面AA1C1C,利用面面垂直的性质;
(Ⅱ)当点E是线段AB1的中点时,有DE∥平面AA1C1C.证明时连结A1B交AB1于点E,连结DE,利用线面平行的判定定理.
(Ⅲ)推理∠C1A1C是二面角C-A1B1-C1的平面角.
(Ⅱ)当点E是线段AB1的中点时,有DE∥平面AA1C1C.证明时连结A1B交AB1于点E,连结DE,利用线面平行的判定定理.
(Ⅲ)推理∠C1A1C是二面角C-A1B1-C1的平面角.
解答:
(本小题满分12分)
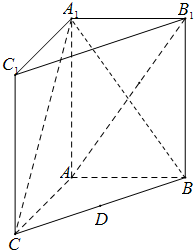
解:(Ⅰ)因为四边形AA1C1C为正方形,所以AA1⊥AC.
因为平面ABC⊥平面AA1C1C,
且平面ABC∩平面AA1C1C=AC,
所以AA1⊥平面ABC.…(4分)(文6分)
(Ⅱ)当点E是线段AB1的中点时,有DE∥平面AA1C1C.
证明:连结A1B交AB1于点E,连结DE.

因为点E是A1B中点,点D是线段BC的中点,
所以DE∥A1C.
又因为DE?平面AA1C1C,A1C?平面AA1C1C,
所以DE∥平面AA1C1C.…(8分)(文12分)
(Ⅲ)因为AA1⊥平面ABC,所以AA1⊥AB.
又因为AC⊥AB,所以AB⊥平面AA1C1C,
所以A1B1⊥平面AA1C1C,
所以A1B1⊥A1C1,A1B1⊥A1C,
所以∠C1A1C是二面角C-A1B1-C1的平面角.
易得tan∠C1A1C=
=1,
所以二面角C-A1B1-C1的平面角为45°.…(12分)

解:(Ⅰ)因为四边形AA1C1C为正方形,所以AA1⊥AC.
因为平面ABC⊥平面AA1C1C,
且平面ABC∩平面AA1C1C=AC,
所以AA1⊥平面ABC.…(4分)(文6分)
(Ⅱ)当点E是线段AB1的中点时,有DE∥平面AA1C1C.
证明:连结A1B交AB1于点E,连结DE.

因为点E是A1B中点,点D是线段BC的中点,
所以DE∥A1C.
又因为DE?平面AA1C1C,A1C?平面AA1C1C,
所以DE∥平面AA1C1C.…(8分)(文12分)
(Ⅲ)因为AA1⊥平面ABC,所以AA1⊥AB.
又因为AC⊥AB,所以AB⊥平面AA1C1C,
所以A1B1⊥平面AA1C1C,
所以A1B1⊥A1C1,A1B1⊥A1C,
所以∠C1A1C是二面角C-A1B1-C1的平面角.
易得tan∠C1A1C=
| C1C |
| C1A1 |
所以二面角C-A1B1-C1的平面角为45°.…(12分)
点评:本题考查面面垂直,考查面面角,解题的关键是掌握面面垂直的判定,考查二面角的定义,解题时要认真审题,注意空间中平行与垂直的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知集合A={x|1<x<3},B={x|x≤2},则集合A∩B( )
| A、(0,1) |
| B、(0,2] |
| C、(1,2) |
| D、(1,2] |
下列说法中,正确的是( )
| A、棱柱的侧面可以是三角形 |
| B、棱柱的侧面是平行四边形,而底面不是平行四边形 |
| C、棱柱的各条棱都相等 |
| D、正方体和长方体都是特殊的四棱柱 |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=