题目内容
已知函数f(x)=loga[(
-2)x+1],(a>0且a≠1,a是参数).
(1)求f(x)的定义域;
(2)当x∈[1,2]时,f(x)>0恒成立;求a的取值范围.
| 1 |
| a |
(1)求f(x)的定义域;
(2)当x∈[1,2]时,f(x)>0恒成立;求a的取值范围.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1))转化(
-2)x+1]>0,(
-2)x>-1,分类讨论求解.
(2)f(x)有意义得:
,再利用函数的性质求解即可.
| 1 |
| a |
| 1 |
| a |
(2)f(x)有意义得:
|
解答:
解:(1)∵(
-2)x+1]>0,(
-2)x>-1,.
当
-2>0时,即0<a<
时,x>
=
定义域为(
,+∞),
当
-2=0时,即=
定义域为R,
当
即a>
且a≠1时,x<
定义域为(-∞,
),
(2)当x∈[1,2]时,f(x)有意义得:
解得0<a<
设t=(
-2)x+1则y=logat关于t是减函数.
①当0<a<
,即
-2≥0,由x∈[1,2],t=(
-2)x+1≥1
∴f(x)=loga[(
-2)x+1]≤0,这与f(x)>0恒成立矛盾.
②当
<a<
,即-
<
-2<0由x∈[1,2]有0<t=(
-2)x+1<1
∴f(x)=loga[(
-2)x+1]>0符合题意,
综上所述:a的取值范围是(
,
)
| 1 |
| a |
| 1 |
| a |
当
| 1 |
| a |
| 1 |
| 2 |
| -1 | ||
|
| a |
| 2a-1 |
| a |
| 2a-1 |
当
| 1 |
| a |
| 1 |
| 2 |
当
|
| 1 |
| 2 |
| a |
| 2a-1 |
| a |
| 2a-1 |
(2)当x∈[1,2]时,f(x)有意义得:
|
| 2 |
| 3 |
设t=(
| 1 |
| a |
①当0<a<
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
∴f(x)=loga[(
| 1 |
| a |
②当
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
∴f(x)=loga[(
| 1 |
| a |
综上所述:a的取值范围是(
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查了指数函数的性质,不等式的求解,属于中档题.

练习册系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的右焦点F是抛物线y2=8x的焦点,两曲线的一个公共点为P,且|PF|=5,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为
,则a=( )
| 1 |
| 2 |
A、
| ||||
B、2或
| ||||
| C、4 | ||||
D、4或
|
下列各组函数中为同一函数的是( )
A、y=(
| ||||||
B、y=|x|与y=
| ||||||
C、f(x)=
| ||||||
| D、y=x与y=a logax |
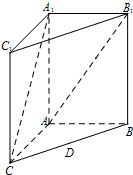 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.