题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
(1)求证:EF∥平面PAD;
(2)求证:面PAB⊥平面PDC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;
(2)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.
(2)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.
解答:
 证明:(1)连接AC,由正方形性质可知,AC与BD相交于BD的中点F,F也为AC中点,E为PC中点.
证明:(1)连接AC,由正方形性质可知,AC与BD相交于BD的中点F,F也为AC中点,E为PC中点.
所以在△CPA中,EF∥PA,
又PA?平面PAD,EF?平面PAD,
所以EF∥平面PAD;
(2)平面PAD⊥平面ABCD
平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA
正方形ABCD中CD⊥ADPA?平面PADCD?平面ABCD
又PA=PD=
AD,所以PA2+PD2=AD2
所以△PAD是等腰直角三角形,且∠APD=
,即PA⊥PD.
因为CD∩PD=D,且CD、PD?面PDC
所以PA⊥面PDC
又PA?面PAB,
所以面PAB⊥面PDC.
 证明:(1)连接AC,由正方形性质可知,AC与BD相交于BD的中点F,F也为AC中点,E为PC中点.
证明:(1)连接AC,由正方形性质可知,AC与BD相交于BD的中点F,F也为AC中点,E为PC中点.所以在△CPA中,EF∥PA,
又PA?平面PAD,EF?平面PAD,
所以EF∥平面PAD;
(2)平面PAD⊥平面ABCD
平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA
正方形ABCD中CD⊥ADPA?平面PADCD?平面ABCD
又PA=PD=
| ||
| 2 |
所以△PAD是等腰直角三角形,且∠APD=
| π |
| 2 |
因为CD∩PD=D,且CD、PD?面PDC
所以PA⊥面PDC
又PA?面PAB,
所以面PAB⊥面PDC.
点评:本题考查直线与平面垂直的判定,直线与平面平行的判定的应用,考查逻辑推理能力.

练习册系列答案
相关题目
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)>0的解集是( )
| A、{x|-3<x<0,或x>3} |
| B、{x|x<-3,或0<x<3} |
| C、{x|x<-3,或x>3} |
| D、{x|-3<x<0,或0<x<3} |
用an表示正整数n的最大奇因数(如a3=3、a10=5),记数列{an}的前n项的和为Sn,则S64值为( )
| A、342 | B、1366 |
| C、2014 | D、5462 |
用1,2,3,4四个数字组成可以有重复数字的三位数有( )个.
| A、4 | B、16 | C、64 | D、256 |
已知双曲线C:
-
=1(a>0,b>0)的右焦点F是抛物线y2=8x的焦点,两曲线的一个公共点为P,且|PF|=5,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
下列各组函数中为同一函数的是( )
A、y=(
| ||||||
B、y=|x|与y=
| ||||||
C、f(x)=
| ||||||
| D、y=x与y=a logax |
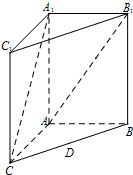 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.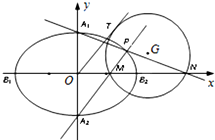 已知椭圆C:
已知椭圆C: