题目内容
若α∈(0,
),比较tan(sinα),tan(tanα),tan(cosα)的大小 .
| π |
| 6 |
考点:三角函数线
专题:计算题,三角函数的求值
分析:作出单位圆,α∈(0,
)时,有cosα>tanα>sinα,tanx在(0,
)上 是增函数,所以tan(cosα)>tan(tanα)>tan(sinα).
| π |
| 6 |
| π |
| 6 |
解答:
解:如图所示:在直角坐标系中,作出单位圆,把角α的顶放到原点,角的始边放到x轴的正半轴上.
设α的终边与单位圆的焦点为B,单位圆和x轴的正半轴的交点为A,
再作BM⊥x轴,M为垂足,则有BM=sinα,OM=cosα,OA=1.

α∈(0,
)时,有cosα>tanα>sinα
因为tanx在(0,
)上 是增函数,所以tan(cosα)>tan(tanα)>tan(sinα),
故答案为:tan(cosα)>tan(tanα)>tan(sinα).
设α的终边与单位圆的焦点为B,单位圆和x轴的正半轴的交点为A,
再作BM⊥x轴,M为垂足,则有BM=sinα,OM=cosα,OA=1.

α∈(0,
| π |
| 6 |
因为tanx在(0,
| π |
| 6 |
故答案为:tan(cosα)>tan(tanα)>tan(sinα).
点评:本题主要考察了三角函数线在解题中的应用,属于基础题.

练习册系列答案
相关题目
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)>0的解集是( )
| A、{x|-3<x<0,或x>3} |
| B、{x|x<-3,或0<x<3} |
| C、{x|x<-3,或x>3} |
| D、{x|-3<x<0,或0<x<3} |
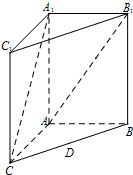 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.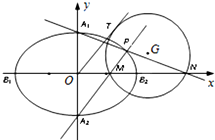 已知椭圆C:
已知椭圆C: