题目内容
已知函数f(x)是定义在R上的偶函数,对于任意x∈R都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有
>0.给出下列命题:
①函数f(x)一定是周期函数;
②函数f(x)在区间[-6,-4]上为增函数;
③直线x=-4是函数f(x)图象的一条对称轴;
④函数f(x)在区间[-6,6]上有且仅有4个零点.
其中正确命题的个数是( )
| f(x1)-f(x2) |
| x1-x2 |
①函数f(x)一定是周期函数;
②函数f(x)在区间[-6,-4]上为增函数;
③直线x=-4是函数f(x)图象的一条对称轴;
④函数f(x)在区间[-6,6]上有且仅有4个零点.
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,令x=-2,易求f(-2)=0,利用f(x)为偶函数可知f(2)=0,于是可得f(x+4)=f(x),可判断①;
②,依题意易知函数f(x)在区间[-6,-4]上为减函数,可判断②;
③,利用偶函数f(x)是周期为4的函数的性质可判断③;
④,利用函数的单调性质及周期性可判断④.
②,依题意易知函数f(x)在区间[-6,-4]上为减函数,可判断②;
③,利用偶函数f(x)是周期为4的函数的性质可判断③;
④,利用函数的单调性质及周期性可判断④.
解答:
解:对于①,∵对于任意x∈R都有f(x+4)=f(x)+f(2)成立,
∴令x=-2,则f(2)=f(-2)+f(2),
∴f(-2)=0,又函数f(x)是定义在R上的偶函数,
∴f(2)=0,
∴f(x+4)=f(x),
∴函数f(x)是周期为4的函数,故①正确;
对于②,∵x1,x2∈[0,2]且x1≠x2时,都有
>0,
∴偶函数y=f(x)在区间[0,2]上是增函数,在[-2,0]上是减函数,又其周期为4,
∴函数f(x)在区间[-6,-4]上为减函数,故②错误;
对于③,∵y=f(x)为偶函数,∴直线x=0(即y轴)是函数f(x)图象的一条对称轴,又函数f(x)是周期为4的函数,
∴直线x=-4是函数f(x)图象的一条对称轴,故③正确;
对于④,∵f(-2)=f(2)=0,函数f(x)是周期为4的函数,
∴f(-6)=f(-2)=0,f(6)=f(2)=0,又y=f(x)在区间[-6,-4],[-2,0],[2,4]上均为减函数;
在区间[-4,-2],[0,2],[4,6]上是增函数,
∴函数f(x)在区间[-6,6]上有且仅有4个零点,故④正确.
综上所述,正确命题的个数是3个,
故选:C.
∴令x=-2,则f(2)=f(-2)+f(2),
∴f(-2)=0,又函数f(x)是定义在R上的偶函数,
∴f(2)=0,
∴f(x+4)=f(x),
∴函数f(x)是周期为4的函数,故①正确;
对于②,∵x1,x2∈[0,2]且x1≠x2时,都有
| f(x1)-f(x2) |
| x1-x2 |
∴偶函数y=f(x)在区间[0,2]上是增函数,在[-2,0]上是减函数,又其周期为4,
∴函数f(x)在区间[-6,-4]上为减函数,故②错误;
对于③,∵y=f(x)为偶函数,∴直线x=0(即y轴)是函数f(x)图象的一条对称轴,又函数f(x)是周期为4的函数,
∴直线x=-4是函数f(x)图象的一条对称轴,故③正确;
对于④,∵f(-2)=f(2)=0,函数f(x)是周期为4的函数,
∴f(-6)=f(-2)=0,f(6)=f(2)=0,又y=f(x)在区间[-6,-4],[-2,0],[2,4]上均为减函数;
在区间[-4,-2],[0,2],[4,6]上是增函数,
∴函数f(x)在区间[-6,6]上有且仅有4个零点,故④正确.
综上所述,正确命题的个数是3个,
故选:C.
点评:本题考查抽象函数的应用,突出考查函数的单调性、周期性、对称性与函数的零点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式(1+x2)(-2x+3)>0的解集是( )
A、{
| ||
B、{x|x<
| ||
C、{x|x>
| ||
D、{x|x>-
|
函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为
,则a=( )
| 1 |
| 2 |
A、
| ||||
B、2或
| ||||
| C、4 | ||||
D、4或
|
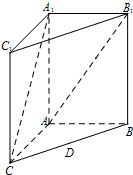 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.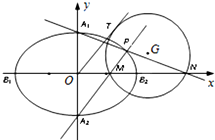 已知椭圆C:
已知椭圆C: