题目内容
已知偶函数f(x)满足对任意x∈R,均有f(1+x)=f(3-x)且f(x)=
,若方程3f(x)=x恰有5个实数解,则实数m的取值范围是 .
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:依题意,可求得偶函数f(x)的图象关于直线x=2对称,是以4为周期的函数,作出y=f(x)的图象后,作图分析即可求得答案.
解答:
解:∵f(1+x)=f(3-x),
∴偶函数f(x)的图象关于直线x=2对称;①,
又f(x)为偶函数,f(-x)=f(x),
∴f(4+x)=f(x),
∴f(x)是以4为周期的函数;②
∵f(x)=
,
方程3f(x)=x恰有5个实数解,
∴y=f(x)的图象与y=
的图象有5个交点,作图如下:
当m=0时,

此时两个函数图象只有3个交点,不满足要求.
当m>0时,

此时m∈(
,
),
同理,当m<0时,m∈(-
,-
),
故实数m的取值范围是:(-
,-
)∪(
,
)
故答案为:(-
,-
)∪(
,
)
∴偶函数f(x)的图象关于直线x=2对称;①,
又f(x)为偶函数,f(-x)=f(x),
∴f(4+x)=f(x),
∴f(x)是以4为周期的函数;②
∵f(x)=
|
方程3f(x)=x恰有5个实数解,
∴y=f(x)的图象与y=
| x |
| 3 |
当m=0时,

此时两个函数图象只有3个交点,不满足要求.
当m>0时,

此时m∈(
| 4 |
| 3 |
| 8 |
| 3 |
同理,当m<0时,m∈(-
| 8 |
| 3 |
| 4 |
| 3 |
故实数m的取值范围是:(-
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
故答案为:(-
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
点评:本题考查抽象函数及其应用,着重考查函数的对称性、周期性的确定及应用,考查转化思想与作图能力,属于难题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
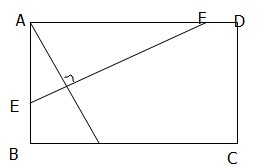 如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.
如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长. 把地球看作半径为R的球,地球上的A、B两地都在北纬45°上,A、B两地的球面距离为
把地球看作半径为R的球,地球上的A、B两地都在北纬45°上,A、B两地的球面距离为