题目内容
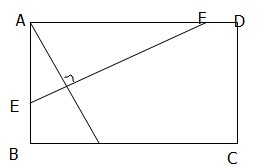如图所示，已知正方形ABCD的边长为32cm，点P在BC上，且BP=16cm，EF⊥AP且与AB、CD分别相交于E、F两点，求EF的长．考点：相似三角形的性质
专题：选作题,立体几何
分析：由勾股定理求AP的长，过E点作EG⊥CD，垂足为G，利用互余关系证明∠BAP=∠GEF，可证△BAP≌△GEF，从而有EF=AP．
解答：
解：在Rt△ABP中，AP=16
，
过E点作EG⊥CD，垂足为G，
∵∠BAP+∠AEF=90°，∠GEF+∠AEF=90°，
∴∠BAP=∠GEF，
又∵AB=BC=EG，∠B=∠EGF=90°，
∴△BAP≌△GEF，
∴EF=AP=16
cm．
解：在Rt△ABP中，AP=16| 5 |
过E点作EG⊥CD，垂足为G，
∵∠BAP+∠AEF=90°，∠GEF+∠AEF=90°，
∴∠BAP=∠GEF，
又∵AB=BC=EG，∠B=∠EGF=90°，
∴△BAP≌△GEF，
∴EF=AP=16
| 5 |
点评：本题考查了全等三角形的判断与性质，正方形的性质及勾股定理的运用．关键是作辅助线，构造全等三角形．
练习册系列答案
相关题目
将形如