题目内容
4.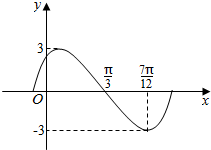 函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.(1)求函数f(x)的解析式及最小正周期;
(2)求f(x)的最大值以及取得最大值时x的取值集合.
分析 (1)利用图象可知函数的周期,进而利用周期公式求得ω;把x=$\frac{π}{3}$代入函数解析式,化简整理求得φ的值,即可得解.
(2)令 2x+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,k∈Z,解得x的值,可得函数的最大值以及取得最大值时x的集合.
解答 解:(1)由图象可得:A=3,其周期为:T=4($\frac{7π}{12}$-$\frac{π}{3}$)=π,由$\frac{2π}{ω}$=π,可得:ω=2,
∵点($\frac{π}{3}$,0)在函数图象上,可得:3sin(2×$\frac{π}{3}$+φ)=0,解得:φ=kπ-$\frac{2π}{3}$,k∈Z,
∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{3}$.
∴函数f(x)的解析式是:y=3sin(2x+$\frac{π}{3}$).
(2)令 2x+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,k∈Z,解得 x=$\frac{π}{12}$+kπ,k∈Z,
可得:函数f(x)的最大值为3,此时,x值的集合为 {x|x=kπ+$\frac{π}{12}$,k∈z}.…(7分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式.考查了学生数形结合思想的运用和对三角函数解析式的理解,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若三点A(4,3),B(5,a),C(6,b)共线,则下列结论正确的是( )
| A. | 2a-b=3 | B. | b-a=1 | C. | a=3,b=5 | D. | a-2b=3 |
9.若$\overrightarrow{OA}$=(3,2),$\overrightarrow{OB}$=(-4,y),并且$\overrightarrow{OB}$⊥$\overrightarrow{OA}$,则|$\overrightarrow{OB}$|=( )
| A. | $\sqrt{13}$ | B. | 4$\sqrt{13}$ | C. | 2$\sqrt{13}$ | D. | 2$\sqrt{11}$ |
13.已知直线(m-1)x+(m2+2m-3)y+m+2=0与两坐标轴有且只有一个交点,则m的值为( )
| A. | 1或-2 | B. | -3或-2 | C. | 1或-3 | D. | 1或-3或-2 |