题目内容
19．若三点A（4，3），B（5，a），C（6，b）共线，则下列结论正确的是（ ）| A． | 2a-b=3 | B． | b-a=1 | C． | a=3，b=5 | D． | a-2b=3 |
分析 三点A（4，3），B（5，a），C（6，b）共线，可得kAB=kAC，解出即可．
解答 解：∵三点A（4，3），B（5，a），C（6，b）共线，
∴kAB=kAC，
∴$\frac{a-3}{5-4}$=$\frac{b-3}{6-4}$，
化为：2a-b=3．
故选：A．
点评 本题考查了三点共线问题、斜率计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
9．设集合$A=\{x|\frac{2}{x+1}≥1\}$，集合B={y|y=2x，x＜0}，则A∩B=（ ）
| A． | （-1，1] | B． | [-1，1] | C． | （0，1） | D． | [-1，+∞） |
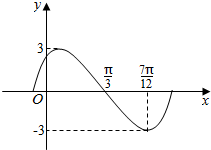函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分如图所示．