题目内容
12.若向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(9,12),$\overrightarrow{n}$=(7,1)且$\overrightarrow{m}$=2$\overrightarrow{a}$-$\overrightarrow{b}$,求向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角的大小.分析 求出向量$\overrightarrow{m}$,通过向量的数量积求解向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角.
解答 解:向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(9,12),$\overrightarrow{n}$=(7,1)且$\overrightarrow{m}$=2$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,-4).
向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为θ,
cosθ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{\left|\overrightarrow{m}\right|\left|\overrightarrow{n}\right|}$=$\frac{-21-4}{\sqrt{(-3)^{2}+({-4)}^{2}}×\sqrt{{7}^{2}+{1}^{2}}}$=$-\frac{\sqrt{2}}{2}$,
θ=135°.
向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角的大小为135°.
点评 本题考查平面向量的数量积的应用,向量的夹角的求法,考查计算能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
3.函数f(x)=2x3+1在[1,1+△x]上的平均变化率为( )
| A. | 3 | B. | 6 | C. | 3+3△x+(△x)2 | D. | 2[3+3△x+(△x)2] |
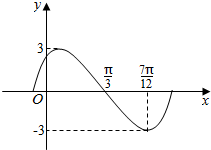 函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.