题目内容
14.已知a,b,c分别为△ABC三个内角A,B,C的对边,且$\sqrt{3}$bsinA=acosB.(1)求B;
(2)求$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4{b}^{2}}$的取值范围.
分析 (1)根据条件及正弦定理便可得到$\sqrt{3}$sinBsinA=sinAcosB,可以得到tanB=$\frac{\sqrt{3}}{3}$,从而得出B;
(2)$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4{b}^{2}}$=$\frac{2abcosC}{4{b}^{2}}$=sinAcosC=sinAcos($\frac{5}{6}$π-A)=-$\frac{1}{2}$sin(2A+$\frac{π}{6}$)+$\frac{1}{4}$,根据A的范围,即可得出结论.
解答 解:(1)∵$\sqrt{3}$bsinA=acosB,
∴$\sqrt{3}$sinBsinA=sinAcosB,
∴tanB=$\frac{\sqrt{3}}{3}$,
∵0<B<π;
∴B=$\frac{π}{6}$;
(2)$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4{b}^{2}}$=$\frac{2abcosC}{4{b}^{2}}$=sinAcosC=sinAcos($\frac{5}{6}$π-A)
=sinA(-$\frac{\sqrt{3}}{2}$cosA+$\frac{1}{2}$sinA)=-$\frac{\sqrt{3}}{4}$sin2A-$\frac{1}{4}$cos2A+$\frac{1}{4}$=-$\frac{1}{2}$sin(2A+$\frac{π}{6}$)+$\frac{1}{4}$,
∵0<A<$\frac{5}{6}$π,
∴$\frac{π}{6}$<2A+$\frac{π}{6}$<$\frac{11}{6}$π,
∴-1≤sin(2A+$\frac{π}{6}$)≤1,
∴-$\frac{1}{4}$≤$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4{b}^{2}}$≤$\frac{3}{4}$.
点评 本题考查正弦定理和余弦定理的运用,考查三角函数知识的运用,考查运算能力,属于中档题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | 是奇函数.非偶函数 | B. | 是偶函数,非奇函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既非奇函数,又非偶函教 |
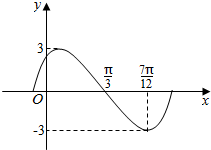 函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.