题目内容
16.抛物线y=x2-4x+3交x轴与M、N点(M在N左边),交y轴于点D,E在第一象限抛物线上,∠EMN=2∠ODM,求E点.分析 根据条件求出M,N,D的坐标,结合三角函数的倍角公式求出直线ME的方程,联立方程组即可求出E的坐标.
解答 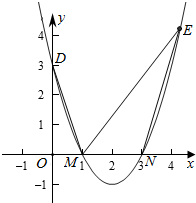 解:∵y=x2-4x+3=(x-1)(x-3),
解:∵y=x2-4x+3=(x-1)(x-3),
∴M(1,0),N(3,0,
当x=0时,y=3,即D(0,3),
则tan∠ODM=$\frac{OM}{OD}$=$\frac{1}{3}$,
设ME的斜率k=tan∠EMN,
∵∠EMN=2∠ODM,
∴tan∠EMN=tan(2∠ODM)=$\frac{2tan∠ODM}{1-ta{n}^{2}∠ODM}$=$\frac{2×\frac{1}{3}}{1-(\frac{1}{3})^{2}}$=$\frac{\frac{2}{3}}{\frac{8}{9}}$=$\frac{3}{4}$,
ME的方程:y=$\frac{3}{4}$(x-1),
由$\frac{3}{4}$(x-1)=(x-1)(x-3),
得(x-1)(x-$\frac{15}{4}$)=0,
得x=$\frac{15}{4}$或 x=1(舍),
此时y=($\frac{15}{4}$-1)×$\frac{3}{4}$=$\frac{11}{4}$×$\frac{3}{4}$=$\frac{33}{16}$,即E($\frac{15}{4}$,$\frac{33}{16}$).
点评 本题主要考查抛物线的方程和应用,根据条件求出坐标,结合三角函数的倍角公式是解决本题的关键.

练习册系列答案
相关题目
6.函数f(x)=$\sqrt{lo{g}_{2}(x-1)}$的定义域为( )
| A. | [2,+∞) | B. | (2,+∞) | C. | (1,+∞) | D. | [1,+∞) |
5.若函数f(x)=x2-$\frac{2}{{x}^{2}}$,则f(x)( )
| A. | 是奇函数.非偶函数 | B. | 是偶函数,非奇函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既非奇函数,又非偶函教 |
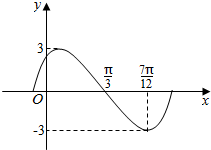 函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.