题目内容
13.已知直线(m-1)x+(m2+2m-3)y+m+2=0与两坐标轴有且只有一个交点,则m的值为( )| A. | 1或-2 | B. | -3或-2 | C. | 1或-3 | D. | 1或-3或-2 |
分析 直线(m-1)x+(m2+2m-3)y+m+2=0与两坐标轴有且只有一个交点,交点必定为原点或斜率k=0或斜率不存在,解出即可得出.
解答 解:∵直线(m-1)x+(m2+2m-3)y+m+2=0与两坐标轴有且只有一个交点,
∴交点必定为原点或斜率k=0或斜率不存在,
∴m+2=0,或$\frac{m-1}{{m}^{2}+2m-3}$=0,或m2+2m-3=0,
解得m=-2,m=-3.(m=1舍去).
故选:B.
点评 本题考查了直线与坐标轴的交点问题,考查了分类讨论与计算能力,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
3.函数f(x)=2x3+1在[1,1+△x]上的平均变化率为( )
| A. | 3 | B. | 6 | C. | 3+3△x+(△x)2 | D. | 2[3+3△x+(△x)2] |
5.若函数f(x)=x2-$\frac{2}{{x}^{2}}$,则f(x)( )
| A. | 是奇函数.非偶函数 | B. | 是偶函数,非奇函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既非奇函数,又非偶函教 |
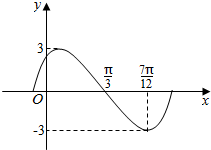 函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.