题目内容

14．已知扇形的圆心角60°，半径为2，则扇形的面积为$\frac{2π}{3}$．

分析 依题意，可求得故其弧长l=θr=π，利用扇形的面积公式S扇=$\frac{1}{2}$lr即可求得答案．

解答 解：依题意知，扇形的圆心角为θ=$\frac{π}{3}$，又半径为2，
故其弧长l=θr=$\frac{2π}{3}$，
所以S扇=$\frac{1}{2}$lr=$\frac{1}{2}$×$\frac{2π}{3}$×2=$\frac{2π}{3}$，
故答案为：$\frac{2π}{3}$．

点评 本题考查扇形的面积公式S扇=$\frac{1}{2}$lr的应用，属于中档题．

练习册系列答案
相关题目
4．设各项都是整数的等差数列{an}的前n项和为Sn，若a1=1且S2、S4-4、S6成等比数列，则（　　）
A．an=4n-3B．an=3n-2C．an=2n-1D．an=n
5．在平面直角坐标系中，若不等式组$\left\{\begin{array}{l}x-y-1≥0\\ ax-y-1≤0\\ x-1≤0\end{array}\right.$（a为常数）所表示的平面区域的面积等于3，则a的值为-5．
2．在△ABC中，$∠A=\frac{π}{3}$，BC=3，点D在BC边上．
（1）若AD为∠A的平分线，且BD=1，求△ABC的面积；
（2）若AD为△ABC的中线，且AD=$\frac{{3\sqrt{3}}}{2}$，求证：△ABC为等边三角形．
9．设集合$A=\{x|\frac{2}{x+1}≥1\}$，集合B={y|y=2x，x＜0}，则A∩B=（　　）
A．（-1，1]B．[-1，1]C．（0，1）D．[-1，+∞）
19．设等差数列{an}的前n项和为Sn，且Sn=$\frac{1}{2}$nan+an-c（c是常数，n∈N*），a2=6．
（Ⅰ）求c的值及数列{an}的通项公式；
（Ⅱ）设bn=$\frac{{{a_n}-2}}{{{2^{n+1}}}}$，数列{bn}的前n项和为Tn，若2Tn＞m-2对n∈N*恒成立，求最大正整数m的值．
6．函数f（x）=$\sqrt{lo{g}_{2}（x-1）}$的定义域为（　　）
A．[2，+∞）B．（2，+∞）C．（1，+∞）D．[1，+∞）
3．函数f（x）=2x3+1在[1，1+△x]上的平均变化率为（　　）
A．3B．6C．3+3△x+（△x）2D．2[3+3△x+（△x）2]
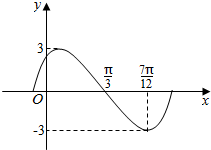4．函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象的一部分如图所示．
（1）求函数f（x）的解析式及最小正周期；
（2）求f（x）的最大值以及取得最大值时x的取值集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网