题目内容
2.已知函数f(x)的定义域为R,当x>0时,f(x)<2,对任意的x,y∈R,f(x)+f(y)=f(x+y)+2成立,若数列{an}满足a1=f(0),且f(an+1)=f($\frac{{a}_{n}}{{a}_{n}+3}$),n∈N*,则a2017的值为( )| A. | 2 | B. | $\frac{6}{2×{3}^{2016}-1}$ | C. | $\frac{2}{2×{3}^{2016}-1}$ | D. | $\frac{2}{2×{3}^{2015}-1}$ |
分析 计算a1,判断f(x)的单调性得出递推公式an+1=$\frac{{a}_{n}}{{a}_{n}+3}$,两边取倒数化简得出∴{$\frac{1}{{a}_{n}}$+$\frac{1}{2}$}是等比数列,从而得出{an}的通项公式.
解答 解:令x=y=0得f(0)=2,∴a1=2.
设x1,x2是R上的任意两个数,且x1<x2,则x2-x1>0,
∵x>0,f(x)<2;
∴f(x2-x1)<2;
即f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-2<2+f(x1)-2=f(x1),
∴f(x)在R上是减函数,
∵f(an+1)=f($\frac{{a}_{n}}{{a}_{n}+3}$),
∴an+1=$\frac{{a}_{n}}{{a}_{n}+3}$,即$\frac{1}{{a}_{n+1}}$=$\frac{3}{{a}_{n}}$+1,
∴$\frac{1}{{a}_{n+1}}$+$\frac{1}{2}$=3($\frac{1}{{a}_{n}}$+$\frac{1}{2}$),
∴{$\frac{1}{{a}_{n}}$+$\frac{1}{2}$}是以1为首项,以3为公比的等比数列,
∴$\frac{1}{{a}_{n}}$+$\frac{1}{2}$=3n-1,
∴an=$\frac{2}{2•{3}^{n-1}-1}$,∴a2017=$\frac{2}{2•{3}^{2016}-1}$.
故选C.
点评 本题主要考查函数与数列的转化,利用抽象函数的关系结合函数的单调性的定义判断函数单调性是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
13.已知数列{an}的各项均为正数,且满足a1=1,$\frac{1}{{a}_{n}^{2}}$-$\frac{1}{{a}_{n-1}^{2}}$=1(n≥2,n∈N*),则a1024=( )
| A. | $\frac{\sqrt{2}}{16}$ | B. | $\frac{1}{16}$ | C. | $\frac{\sqrt{2}}{32}$ | D. | $\frac{1}{32}$ |
10.在平面直角坐标系内,区域M满足$\left\{\begin{array}{l}0≤x≤π\\ 0≤y≤1\end{array}$区域N满足$\left\{\begin{array}{l}0≤x≤π\\ 0≤y≤sinx\end{array}$则向区域M内投一点,落在区域N内的概率是( )
| A. | $\frac{2}{π}$ | B. | $\frac{π}{4}$ | C. | 2-$\frac{2}{π}$ | D. | 2-$\frac{π}{4}$ |
14.已知正方形ABCD的边长为2,E是BC的中点,以点C为圆心,CE长为半径作圆,点P是该圆上的任一点,则$\overrightarrow{AP}•\overrightarrow{DE}$的取值范围是( )
| A. | $[0,2+\sqrt{6}]$ | B. | $[2-\sqrt{6},2+\sqrt{6}]$ | C. | $[0,2+\sqrt{5}]$ | D. | $[2-\sqrt{5},2+\sqrt{5}]$ |
12.在区间[-4,1]上随机地取一个实数x,若x满足|x|<a的概率为$\frac{4}{5}$,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
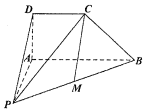 如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.
如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.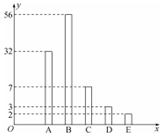 某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题: