题目内容
11.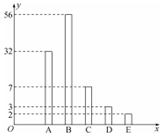 某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:(1)试估算该校高三年级学生获得成绩为B的人数;
(2)若等级A、B、C、D、E分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?
(3)以每个学生的心理都培养成为健康状态为目标,学校决定对成绩等级为E的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率..
分析 (1)从条形图中可知这100人中,有56名学生成绩等级为B,由此可以估计该校学生获得成绩等级为B的概率,从而能求出该校高三年级学生获得成绩等级为B的人数.
(2)这100名学生成绩的平均分为91.3分,由91.3>90,得到该校高三年级目前学生的“考前心理稳定整体”已过关.
(3)按分层抽样抽取的4人中有1名男生,3名女生,记男生为a,3名女生分别为b1,b2,b3.利用列举法能求出从中抽取2人其中恰好抽到1名男生的概率.
解答 解:(1)从条形图中可知这100人中,有56名学生成绩等级为B,
故可以估计该校学生获得成绩等级为B的概率为$\frac{56}{100}=\frac{14}{25}$,
则该校高三年级学生获得成绩等级为B的人数约有$800×\frac{14}{25}=448$.
(2)这100名学生成绩的平均分为$\frac{1}{100}(32×100+56×90+7×80+3×70+2×60)$=91.3(分),
因为91.3>90,所以该校高三年级目前学生的“考前心理稳定整体”已过关.
(3)按分层抽样抽取的4人中有1名男生,3名女生,记男生为a,3名女生分别为b1,b2,b3.
从中抽取2人的所有情况为ab1,ab2,ab3,b1b2,b1b3,b2b3,共6种情况,
其中恰好抽到1名男生的有ab1,ab2,ab3,共3种情况,故所求概率$P=\frac{1}{2}$.
点评 本题考查条形图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
2.已知函数f(x)的定义域为R,当x>0时,f(x)<2,对任意的x,y∈R,f(x)+f(y)=f(x+y)+2成立,若数列{an}满足a1=f(0),且f(an+1)=f($\frac{{a}_{n}}{{a}_{n}+3}$),n∈N*,则a2017的值为( )
| A. | 2 | B. | $\frac{6}{2×{3}^{2016}-1}$ | C. | $\frac{2}{2×{3}^{2016}-1}$ | D. | $\frac{2}{2×{3}^{2015}-1}$ |
19.已知函数$f(x)=x-{e^{\frac{x}{a}}}$(a>0),且y=f(x)的图象在x=0处的切线l与曲y=ex相切,符合情况的切线( )
| A. | 有0条 | B. | 有1条 | C. | 有2条 | D. | 有3条 |
16.已知定义在(0,+∞)上的函数f(x)的导函数f'(x)满足$xf'(x)+f(x)=\frac{lnx}{x}$,且$f(e)=\frac{1}{e}$,其中e为自然对数的底数,则不等式$f(x)+e>x+\frac{1}{e}$的解集是( )
| A. | $(0,\frac{1}{e})$ | B. | (0,e) | C. | $(\frac{1}{e},e)$ | D. | $(\frac{1}{e},+∞)$ |
1.下列不等式中,与不等式$\frac{x+4}{{{x^2}-2x+2}}>3$的解集相同的是( )
| A. | (x+4)(x2-2x+2)>3 | B. | x+4>3(x2-2x+2) | C. | $\frac{1}{{{x^2}-2x+2}}>\frac{3}{x+4}$ | D. | $\frac{{{x^2}-2x+2}}{x+4}<\frac{1}{3}$ |