题目内容
求过两点A（1，0），B（2，1），且圆心在直线x-y=0上的圆的标准方程．
考点：圆的标准方程
专题：计算题,直线与圆
分析：根据A、B的坐标算出AB的斜率k=1，线段AB的中点为(
，
)，进而算出线段AB中垂线的方程为y=-x+2．由题意得圆心C为AB的中垂线与直线x-y=0的交点，联解两直线的方程得圆心为C（1，1），再利用两间点的距离公式算出半径r=1，可得所求圆的标准方程．
| 3 |
| 2 |
| 1 |
| 2 |
解答：
解：∵点A（1，0）、B（2，1），
∴直线AB的斜率为k=
=1，线段AB的中点为(
，
)，
由此可得AB的垂直平分线的斜率k'=
=-1
∴线段AB的垂直平分线的方程为y-
=-(x-
)，化简得y=-x+2，
∵点A、B在圆上，且圆心在直线x-y=0上，
∴解方程组
，得
，
可得圆心的坐标为（1，1），
圆的半径为r=|AC|=
=1，
∴所求圆的标准方程为（x-1）2+（y-1）2=1．
∴直线AB的斜率为k=
| 1-0 |
| 2-1 |
| 3 |
| 2 |
| 1 |
| 2 |
由此可得AB的垂直平分线的斜率k'=
| -1 |
| k |
∴线段AB的垂直平分线的方程为y-
| 1 |
| 2 |
| 3 |
| 2 |
∵点A、B在圆上，且圆心在直线x-y=0上，
∴解方程组
|
|
可得圆心的坐标为（1，1），
圆的半径为r=|AC|=
| (1-1)2+(1-0)2 |
∴所求圆的标准方程为（x-1）2+（y-1）2=1．
点评：本题求经过定点A、B，且圆心在定直线上的圆方程．着重考查了直线的基本量与基本形式、两点间的距离公式、圆的标准方程等知识，属于基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V1．直径为4的球的体积为V2，则V1：V2=（ ）| A、1：4 | B、1：2 |
| C、1：1 | D、2：1 |
定义域为R的函数f（x）满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x2-x，则当x∈[-1，0]时，f（x）的最小值为（ ）
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
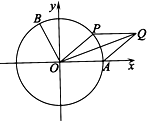如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B，P在单位圆上，且