Question

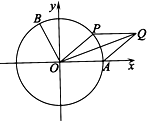如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B，P在单位圆上，且B(-

5

5

，

2 5

5

)，∠AOB=α．
（1）求

4cosα-3sinα

5cosα+3sinα

的值；
（2）设∠AOP=θ(

π

6

≤θ≤

2

3

π)，

OQ

=

OA

+

OP

，四边形OAQP的面积为S，f(θ)=(

OA

•

OQ

-1)2+

2

S-1，求f（θ）的最值及此时θ的值．

Answer 1

考点：三角函数的最值,三角函数的化简求值,三角函数中的恒等变换应用

专题：计算题,三角函数的求值

分析：（1）依题意，可求得tanα=2，将

4cosα-3sinα

5cosα+3sinα

中的“弦”化“切”即可求得其值；
（2）利用向量的数量积的坐标运算可求得f（θ）=-sin²θ+

2

sinθ；θ∈[

π

6

，

2π

3

]⇒

1

2

≤sinθ≤1，利用正弦函数的单调性与最值即可求得f（θ）的最值及此时θ的值．

解答： 解：（1）依题意，tanα=

2 5 5

- 5 5

=-2，
∴

4cosα-3sinα

5cosα+3sinα

=

4-3tanα

5+3tanα

=

4-3×(-2)

5+3×(-2)

=-10；
（2）由已知点P的坐标为P（cosθ，sinθ），
又

OQ

=

OA

+

OP

，|

OA

|=|

OP

|，
∴四边形OAQP为菱形，
∴S=2S_△OAP=sinθ，
∵A（1，0），P（cosθ，sinθ），
∴

OQ

=（1+cosθ，sinθ），
∴

OA

•

OQ

=1+cosθ，
∴f（θ）=（1+cosθ-1）²+

2

sinθ-1
=cos²θ+

2

sinθ-1
=-sin²θ+

2

sinθ，
∵

1

2

≤sinθ≤1，
∴当sinθ=

2

2

，即θ=

π

4

时，f（θ）_max=

1

2

；
当sinθ=1，即θ=

π

2

时，f（θ）_max=

2

-1．

点评：本题考查三角函数的最值，着重考查三角函数中的恒等变换应用及向量的数量积的坐标运算，考查正弦函数的单调性及最值，属于中档题．